题目内容
已知:命题p:1≤x≤3;命题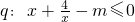 ,当p是q的充分条件时,实数m的取值范围是________.
,当p是q的充分条件时,实数m的取值范围是________.
[5,+∞)
分析:将p是q的充分条件转化为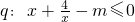 在1≤x≤3恒成立,分离出m转化为求函数的最大值,利用导数判断出
在1≤x≤3恒成立,分离出m转化为求函数的最大值,利用导数判断出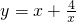 的单调性,求出函数的最大值.
的单调性,求出函数的最大值.
解答:因为p是q的充分条件,
所以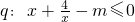 在1≤x≤3恒成立,
在1≤x≤3恒成立,
所以 在1≤x≤3恒成立,
在1≤x≤3恒成立,
所以 即可
即可
令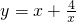 ,
,

当1<x<2时,y′<0,当2<x<3时,y′>0,
当x=1时,y=5;当x=3时,y=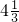
所以m≥5
故答案为[5,+∞)
点评:解决不等式恒成立问题,一般利用的方法是分离参数转化为求函数的最值,本题的关键是将p是q的充分条件转化为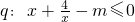 在1≤x≤3恒成立.
在1≤x≤3恒成立.
分析:将p是q的充分条件转化为
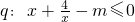 在1≤x≤3恒成立,分离出m转化为求函数的最大值,利用导数判断出
在1≤x≤3恒成立,分离出m转化为求函数的最大值,利用导数判断出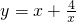 的单调性,求出函数的最大值.
的单调性,求出函数的最大值.解答:因为p是q的充分条件,
所以
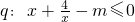 在1≤x≤3恒成立,
在1≤x≤3恒成立,所以
 在1≤x≤3恒成立,
在1≤x≤3恒成立,所以
 即可
即可令
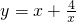 ,
,
当1<x<2时,y′<0,当2<x<3时,y′>0,
当x=1时,y=5;当x=3时,y=
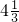
所以m≥5
故答案为[5,+∞)
点评:解决不等式恒成立问题,一般利用的方法是分离参数转化为求函数的最值,本题的关键是将p是q的充分条件转化为
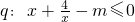 在1≤x≤3恒成立.
在1≤x≤3恒成立. 
练习册系列答案
相关题目
 (
( ),
), 的最小值;
的最小值; ,命题p:关于x的不等式
,命题p:关于x的不等式 对任意
对任意 对任意
对任意 恒成立.若“p或q”为真,“p且q”为假,求实数m的取值范围.
恒成立.若“p或q”为真,“p且q”为假,求实数m的取值范围. ,当p是q的充分条件时,实数m的取值范围是 .
,当p是q的充分条件时,实数m的取值范围是 .