题目内容
(本题满分16分)已知定义在 上的函数
上的函数 ,其中
,其中 为常数.
为常数.
(1)若 是函数
是函数 的一个极值点,求
的一个极值点,求 的值;
的值;
(2)若函数 在区间
在区间 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;
(3)若函数 ,在
,在 处取得最大值,求正数
处取得最大值,求正数 的取值范围.
的取值范围.
【答案】
解:(1)因为 是函数
是函数 的一个极值点,
的一个极值点,
所以 ,即
,即 ,………2分
,………2分
经检验,当 时,
时, 是函数
是函数 的一个极值点. ………3分
的一个极值点. ………3分
(2)由题, 在
在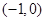 恒成立,
………5分
恒成立,
………5分
即 在
在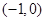 恒成立,所以
恒成立,所以 , ………6分
, ………6分
又因为 在
在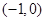 恒成立上递减,所以当
恒成立上递减,所以当 时,
时, , ………7分
, ………7分
所以 .
………8分
.
………8分
(3)由题, 在
在 上恒成立且等号必能取得,
上恒成立且等号必能取得,
即 -----(*)在
-----(*)在 上恒成立且等号必能取得,………10分
上恒成立且等号必能取得,………10分
当 时,不等式(*)显然恒成立且取得了等号
………11分
时,不等式(*)显然恒成立且取得了等号
………11分
当 时,不等式(*)可化得
时,不等式(*)可化得 ,所以
,所以 ………12分
………12分
考察函数
令 ,则
,则 ,所以
,所以 ,
,
因为函数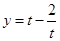 在
在 上递增,所以当
上递增,所以当 时,
时, ………14分
………14分
所以 ,又因为
,又因为 ,所以
,所以 .
………16分
.
………16分
【解析】略

练习册系列答案
相关题目
 ,且对任意
,且对任意 ,有
,有 .
. ;
; 在区间(0,1)上为单调函数,求实
在区间(0,1)上为单调函数,求实 数
数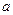 的取值范围.
的取值范围. 的零点个数?(提示
的零点个数?(提示 )
) 为实常数).
为实常数). 时,求函数
时,求函数 在
在 上的最小值;
上的最小值; 在区间
在区间 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
 )
) :
: 的离心率为
的离心率为 ,
, 分别为椭圆
分别为椭圆 为椭圆上任意一点,以
为椭圆上任意一点,以 为半径作圆
为半径作圆 有公共点时,求△
有公共点时,求△ 面积的最大值.
面积的最大值. 是定义在
是定义在 上的偶函数,且当
上的偶函数,且当 时,
时, 。
。 及
及 的值;
的值; 上的解析式;
上的解析式; 的方程
的方程 有四个不同的实数解,求实数
有四个不同的实数解,求实数 的取值范围。
的取值范围。