题目内容
已知等比数列{an}满足2a1+a3=3a2，且a3+2是a2，a4的等差中项．（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若
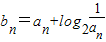，Sn=b1+b2+…bn，求使 
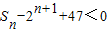成立的正整数n的最小值．
【答案】分析：（Ⅰ）设等比数列{an}的首项为a1，公比为q，根据2a1+a3=3a2，且a3+2是a2，a4的等差中项，建立方程组，从而可求数列{an}的通项公式；
（Ⅱ）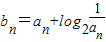
=2n-n，求出Sn=b1+b2+…bn，再利用
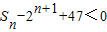，建立不等式，即可求得使
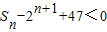成立的正整数n的最小值．
解答：解：（Ⅰ）设等比数列{an}的首项为a1，公比为q，
依题意，∵2a1+a3=3a2，且a3+2是a2，a4的等差中项
∴
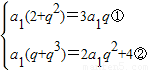
由 ①得 q2-3q+2=0，解得q=1或q=2．
当q=1时，不合题意舍；
当q=2时，代入（2）得a1=2，所以an=2n．…．…（6分）
（Ⅱ）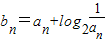
=2n-n．…．…（7分）
所以Sn=b1+b2+…bn=（2+22++2n）-（1+2+…+n）=2n+1-2-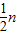
-
n2 …．…（10分）
因为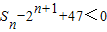
，所以2n+1-2-
-
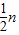n2-2n+1+47＜0，
即n2+n-90＞0，解得n＞9或n＜-10．…．…（12分）
故使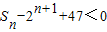
成立的正整数n的最小值为10．…．（13分）
点评：本题考查等比数列的通项，考查数列的通项与求和，考查解不等式，解题的关键是确定数列的通项与和，属于中档题．
（Ⅱ）
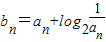=2n-n，求出Sn=b1+b2+…bn，再利用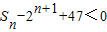，建立不等式，即可求得使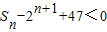成立的正整数n的最小值．解答：解：（Ⅰ）设等比数列{an}的首项为a1，公比为q，
依题意，∵2a1+a3=3a2，且a3+2是a2，a4的等差中项
∴
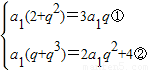
由 ①得 q2-3q+2=0，解得q=1或q=2．
当q=1时，不合题意舍；
当q=2时，代入（2）得a1=2，所以an=2n．…．…（6分）
（Ⅱ）
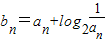=2n-n．…．…（7分）所以Sn=b1+b2+…bn=（2+22++2n）-（1+2+…+n）=2n+1-2-
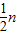-n2 …．…（10分）因为
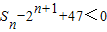，所以2n+1-2-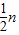-n2-2n+1+47＜0，即n2+n-90＞0，解得n＞9或n＜-10．…．…（12分）
故使
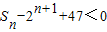成立的正整数n的最小值为10．…．（13分）点评：本题考查等比数列的通项，考查数列的通项与求和，考查解不等式，解题的关键是确定数列的通项与和，属于中档题．
练习册系列答案
期末集结号系列答案
相关题目