题目内容
f(x)= sin(ωx+φ)+cos (ωx+φ) (ω>0,
sin(ωx+φ)+cos (ωx+φ) (ω>0, <
< 的最小正周期为π,且f(-x)=f(x),则下列关于g(x)= sin(ωx+φ)的图象说法正确的是( )
的最小正周期为π,且f(-x)=f(x),则下列关于g(x)= sin(ωx+φ)的图象说法正确的是( )
A.函数在x∈[ ]上单调递增 ]上单调递增 |
B.关于直线x= 对称 对称 |
C.在x∈[0, ]上,函数值域为[0,1] ]上,函数值域为[0,1] |
D.关于点 对称 对称 |
B
解析试题分析:根据题意,由于f(x)= sin(ωx+φ)+cos (ωx+φ) =2sin(ωx+φ+
sin(ωx+φ)+cos (ωx+φ) =2sin(ωx+φ+ ) (ω>0,
) (ω>0, <
< 的最小正周期为π,可知w=2,同时且f(-x)=f(x),说明是偶函数,则可知φ+
的最小正周期为π,可知w=2,同时且f(-x)=f(x),说明是偶函数,则可知φ+ =
=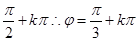 ,故可知
,故可知 ,因此可知g(x)= sin(ωx+φ)=sin(2x+
,因此可知g(x)= sin(ωx+φ)=sin(2x+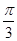 ),那么可知函数在x∈[
),那么可知函数在x∈[ ]上单调递增,成立,对于在x∈[0,
]上单调递增,成立,对于在x∈[0, ]上,函数值域为[0,1],根据整体的性质可知,满足题意,对于关于点
]上,函数值域为[0,1],根据整体的性质可知,满足题意,对于关于点 对称,即将x=
对称,即将x= 代入,函数值为零成立,故排除法选B。
代入,函数值为零成立,故排除法选B。
考点:三角函数的性质
点评:本题考查命题的真假判断,解题时要认真审题,注意三角函数的性质的合理运用.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
关于函数 的四个结论:P1:最大值为
的四个结论:P1:最大值为 ;P2:把函数
;P2:把函数 的图象向右平移
的图象向右平移 个单位后可得到函数
个单位后可得到函数 的图象; P3:单调递增区间为[
的图象; P3:单调递增区间为[ ],
], ; P4:图象的对称中心为(
; P4:图象的对称中心为( ),
), .其中正确的结论有
.其中正确的结论有
| A.1个 | B.2个 | C.3个 | D.4个 |
下列各式中,值为 的是( )
的是( )
A. | B. |
C. | D. |
为了得到函数 的图象,可将函数
的图象,可将函数 的图象( )
的图象( )
A.向左平移 个长度单位 个长度单位 | B.向左平移 个长度单位 个长度单位 |
C.向右平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
要得到函数 的导函数
的导函数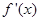 的图象,只需将
的图象,只需将 的图象( )
的图象( )
A.向左平移 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) |
B.向左平移 个单位,再把各点的纵坐标缩短到原来的 个单位,再把各点的纵坐标缩短到原来的 倍(横坐标不变) 倍(横坐标不变) |
C.向左平移 个单位,再把各点的纵坐标伸长到原来的 个单位,再把各点的纵坐标伸长到原来的 倍(横坐标不变) 倍(横坐标不变) |
D.向左平移 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变) |
已知 =
=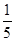 ,0<x<π,则tanx为
,0<x<π,则tanx为
A.- | B.- | C.2 | D.-2 |
为了得到函数 的图象,可以将函数
的图象,可以将函数 的图象( )
的图象( )
A.向右平移 个长度单位 个长度单位 | B.向左平移 个长度单位 个长度单位 |
C.向右平移 个长度单位 个长度单位 | D.向左平移 个长度单位 个长度单位 |
要得到 的图象,只需把
的图象,只需把 的图象
的图象
A.向右平移 个单位 个单位 | B.向左平移 个单位 个单位 |
C.向右平移 个单位 个单位 | D.向左平移 个单位 个单位 |
 等于( )
等于( )
A. | B. | C.- | D.- |