题目内容
若 A(m+1,n-1,3),B (2m,n,m-2n),C( m+3,n-3,9)三点共线,则M+n=________.
0
分析:根据点A,B,C的坐标,分别求出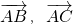 的坐标,利用三点共线,可建立方程组,从而可求m+n的值
的坐标,利用三点共线,可建立方程组,从而可求m+n的值
解答:由题意,∵A(m+1,n-1,3),B (2m,n,m-2n),C( m+3,n-3,9)
∴
∵A(m+1,n-1,3),B (2m,n,m-2n),C( m+3,n-3,9)三点共线,
∴
∴(m-1,1,m-2n-3)=λ(2,-2,6)
∴
∴
∴m+n=0
故答案为:0
点评:本题以点为载体,考查三点共线,解题的关键是求向量的坐标,利用向量共线的条件.
分析:根据点A,B,C的坐标,分别求出
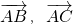 的坐标,利用三点共线,可建立方程组,从而可求m+n的值
的坐标,利用三点共线,可建立方程组,从而可求m+n的值解答:由题意,∵A(m+1,n-1,3),B (2m,n,m-2n),C( m+3,n-3,9)
∴

∵A(m+1,n-1,3),B (2m,n,m-2n),C( m+3,n-3,9)三点共线,
∴

∴(m-1,1,m-2n-3)=λ(2,-2,6)
∴

∴

∴m+n=0
故答案为:0
点评:本题以点为载体,考查三点共线,解题的关键是求向量的坐标,利用向量共线的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数
 为奇函数,则m、n的值为
为奇函数,则m、n的值为
[
]|
A .m=1,n=2 |
B .m=-1,n=2 |
|
C .m±1,n=2 |
D .m±1,nÎ R |
若函数 为奇函数,则m、n的值为
为奇函数,则m、n的值为
[ ]
|
A.m=1,n=2 |
B.m=-1,n=2 |
|
C.m±1,n=2 |
D.m±1,nÎ R |