题目内容
3.抛物线y2=4x上一点P和焦点F的距离等于5,则点P的坐标是(4,4),(4,-4).分析 设P(m,n),求出抛物线的准线方程,运用抛物线的定义可得m+1=5,即可解得m,再由抛物线方程,可得n,进而得到P的坐标.
解答 解:设P(m,n),
由于抛物线y2=4x的准线为x=-1,
则由定义可得|PF|=m+1=5,
解得m=4,
则n2=16,解得n=-4和4.
即有P(4,4)或(4,-4).
故答案为:(4,4),(4,-4).
点评 本题考查抛物线的定义、方程和性质,主要考查抛物线的准线方程的运用,运用定义是解题的关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
在一次篮球定点投篮训练中,规定每人最多投3次,在 处每投进一球得3分;在
处每投进一球得3分;在 处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次.某同学在
处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次.某同学在 处的投中率
处的投中率 ,在
,在 处的投中率为
处的投中率为 ,该同学选择先在
,该同学选择先在 处投第一球,以后都在
处投第一球,以后都在 处投,且每次投篮都互不影响,用
处投,且每次投篮都互不影响,用 表示该同学投篮训练结束后所得的总分,其分布列为:
表示该同学投篮训练结束后所得的总分,其分布列为:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求 的值;
的值;
(2)求随机变量 的数学期望
的数学期望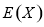 ;
;
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小.
11.已知函数f(x)=$\left\{\begin{array}{l}{x+3,x>a}\\{{x}^{2}+6x+3,x≤a}\end{array}\right.$函数g(x)=f(x)-2x恰有三个不同的零点,则实数a的取值范围是( )
| A. | [-1,3) | B. | [-3,-1] | C. | [-3,3) | D. | [-1,1) |
 为奇函数,
为奇函数, 为常数.
为常数. 的值;
的值; 的单调性,并写出单调区间;
的单调性,并写出单调区间; 的前
的前 项和
项和 ,
,
 ,数列
,数列 满足
满足 .
. 的通项公式;
的通项公式; ,使得
,使得 为等比数列?并说明理由.
为等比数列?并说明理由. 则
则 ( )
( ) B.
B. C.
C. D.
D.





