题目内容
函数 的最小值为
的最小值为
- A.2
- B.

- C.1
- D.不存在
B
分析:要求函数 的最小值,本题形式可以变为用基本不等式求函数最值,用此法时要注意验证等号成立的条件是不是具备.
的最小值,本题形式可以变为用基本不等式求函数最值,用此法时要注意验证等号成立的条件是不是具备.
解答:由于 =
= =
=
令t=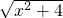 ,则t≥2,f(t)=t
,则t≥2,f(t)=t 在(2,+∞)上单调递增,
在(2,+∞)上单调递增,
∴ 的最小值为:
的最小值为:
故选B.
点评:本题的考点是函数的最值及其几何意义,考查分式形函数求最值的方法,本题分子次数高于分母次数,故将其恒等变形为可以用基本不等式求最值的形式,求最值,这是解此类题求最值优先选用的方法,本题有一易错点,那就是忘记验证等号成立的条件是否在定义域内,属中档题.
分析:要求函数
 的最小值,本题形式可以变为用基本不等式求函数最值,用此法时要注意验证等号成立的条件是不是具备.
的最小值,本题形式可以变为用基本不等式求函数最值,用此法时要注意验证等号成立的条件是不是具备.解答:由于
 =
= =
=
令t=
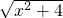 ,则t≥2,f(t)=t
,则t≥2,f(t)=t 在(2,+∞)上单调递增,
在(2,+∞)上单调递增,∴
 的最小值为:
的最小值为:
故选B.
点评:本题的考点是函数的最值及其几何意义,考查分式形函数求最值的方法,本题分子次数高于分母次数,故将其恒等变形为可以用基本不等式求最值的形式,求最值,这是解此类题求最值优先选用的方法,本题有一易错点,那就是忘记验证等号成立的条件是否在定义域内,属中档题.

练习册系列答案
相关题目
 的最小值为
的最小值为  C.4
D.6
C.4
D.6