题目内容
已知实数x,y满足不等式组Ω:
(Ⅰ)作出不等式组Ω所表示的平面区域.
(Ⅱ)求z=3x-2y的最大值;
(Ⅲ)求t=
的最小值.
|
(Ⅰ)作出不等式组Ω所表示的平面区域.
(Ⅱ)求z=3x-2y的最大值;
(Ⅲ)求t=
| x2+y2 |
分析:(Ⅰ)利用二元一次不等式组表示平面区域,作出不等式组Ω所表示的平面区域.
(Ⅱ)利用z的几何意义,求z=3x-2y的最大值;
(Ⅲ)利用t的几何意义,求t=
的最小值.
(Ⅱ)利用z的几何意义,求z=3x-2y的最大值;
(Ⅲ)利用t的几何意义,求t=
| x2+y2 |
解答: 解:(Ⅰ)可行域如图所示:
解:(Ⅰ)可行域如图所示:
(Ⅱ)令直线l:y=
x-
z,
则当直线l过点C(2,0)时,l的纵截距-
z取最小值,
此时z取最大值,且最大值为4.
(ⅱ)t=
表示可行域内的点(x,y)与原点O的距离.
过原点O作直线x+y=2的垂线,易知垂足在可行域上,
∴所求的最小值为tmin=
=
.
 解:(Ⅰ)可行域如图所示:
解:(Ⅰ)可行域如图所示:(Ⅱ)令直线l:y=
| 3 |
| 2 |
| 1 |
| 2 |
则当直线l过点C(2,0)时,l的纵截距-
| 1 |
| 2 |
此时z取最大值,且最大值为4.
(ⅱ)t=
| x2+y2 |
过原点O作直线x+y=2的垂线,易知垂足在可行域上,
∴所求的最小值为tmin=
| 2 | ||
|
| 2 |
点评:本题主要考查线性规划的知识,利用目标函数的几何意义,是解决线性规划的基本方法,注意结合数形结合的思想进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则目标函数z=x-y的最大值等于( )
,则目标函数z=x-y的最大值等于( )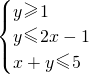 ,则目标函数z=x-y的最大值等于________.
,则目标函数z=x-y的最大值等于________. ,则目标函数z=x-y的最大值等于 .
,则目标函数z=x-y的最大值等于 .