题目内容

已知0＜x＜
π
2
，用单位圆求证下面的不等式：
（1）sinx＜x＜tanx；
（2）sin
1
2
•sin
2
3
•sin
3
4
•…•sin
2010
2011
＜
1
2010
．
分析：（1）利用单位圆中的三角函数线，通过面积关系证明sinx＜x＜tanx；
（2）利用（1）的结论，采用放缩法，求出sin
1
2
•sin
2
3
•sin
3
4
••sin
2010
2011
＜
1
2
•
2
3
•
3
4
••
2010
2011
=
1
2011
＜
1
2010
推出结果．
解答：精英家教网证明：（1）如图，在单位圆中，有sinx=MA，cosx=OM，
tanx=NT，连接AN，则S△OAN＜S扇形OAN＜S△ONT，
设
AN
的长为l，则x=
l
r
=l，
∴
1
2
ON•MA＜
1
2
ON•x＜
1
2
ON•NT，即MA＜x＜NT，
又sinx=MA，cosx=OM，tanx=NT，
∴sinx＜x＜tanx；

（2）∵
1
2
，
2
3
，
3
4
，，
2010
2011
均为小于
π
2
的正数，由（1）中的sinx＜x得，sin
1
2
＜
1
2
，sin
2
3
＜
2
3
，sin
3
4
＜
3
4
，，sin
2010
2011
＜
2010
2011
，
将以上2010道式相乘得sin
1
2
•sin
2
3
•sin
3
4
••sin
2010
2011
＜
1
2
•
2
3
•
3
4
••
2010
2011
=
1
2011
＜
1
2010
，
即sin
1
2
•sin
2
3
•sin
3
4
••sin
2010
2011
＜
1
2010
．
点评：本题考查单位圆的应用，不等式的证明的方法，考查分析问题解决问题的能力，是中档题．
练习册系列答案
相关题目
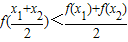给出下列四个命题：
①函数f（x）=2x-x2有且仅有两个零点；
②对于函数f（x）=lnx的定义域中任意的x1，x2（x1≠x2）必有f(
x1+x2
2
)＜
f(x1)+f(x2)
2
；
③已知f（x）=|2-x-1|，当a＜b时有f（a）＜f（b），则必有0＜f（b）＜1；
④已知图象连续不断的函数y=f（x）在区间（a，b）（b-a=0.1）上有唯一零点，如果用“二分法”求这个零点（精确度0.0001）的近似值，那么将区间（a，b）等分的次数至少是10次．
其中正确命题的序号是
③④
③④
．

已知函数f(x)＝．

(1)用定义证明函数f(x)在(－∞，＋∞)上为减函数；

(2)若x∈[1，2]，求函数f(x)的值域；

(3)若g(x)＝＋f(x)，且当x∈[1，2]时g(x)≥0恒成立，求实数a的取值范围．
给出下列四个命题：
①函数f（x）=2x-x2有且仅有两个零点；
②对于函数f（x）=lnx的定义域中任意的x1，x2（x1≠x2）必有；
③已知f（x）=|2-x-1|，当a＜b时有f（a）＜f（b），则必有0＜f（b）＜1；
④已知图象连续不断的函数y=f（x）在区间（a，b）（b-a=0.1）上有唯一零点，如果用“二分法”求这个零点（精确度0.0001）的近似值，那么将区间（a，b）等分的次数至少是10次．
其中正确命题的序号是    ．
给出下列四个命题：
①函数f（x）=2x-x2有且仅有两个零点；
②对于函数f（x）=lnx的定义域中任意的x1，x2（x1≠x2）必有；
③已知f（x）=|2-x-1|，当a＜b时有f（a）＜f（b），则必有0＜f（b）＜1；
④已知图象连续不断的函数y=f（x）在区间（a，b）（b-a=0.1）上有唯一零点，如果用“二分法”求这个零点（精确度0.0001）的近似值，那么将区间（a，b）等分的次数至少是10次．
其中正确命题的序号是    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网