题目内容

已知点Pn(an,bn)满足：an+1=an·bn+1,bn+1=,n∈N,且已知P0(,).

(1)求过P0、P1的直线l的方程；

（2）判断点Pn(n≥2)与直线l的位置关系，并证明你的结论.

解：(1)由a0=,b0=,得

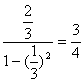b1=,a1=×=.

显然直线l的方程为x+y=1.

(2)由a1=,b1=,得

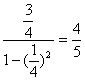b2=,a2=×.

∴点P2∈l,猜想点Pn(n≥2)在直线l上，

以下用数学归纳法证明：

当n=2时，点P2∈l,

假设当n=k(k≥2)时,点Pk∈l,即

ak+bk=1,

当n=k+1时，

ak+1+bk+1=ak·bk+1+bk+1=(1+ak)bk+1

=(1+ak)=1.

∴点Pk+1∈l.

综上，点Pn∈l(n≥2).

练习册系列答案
相关题目
（理）已知点A（1，0），B（0，1）和互不相同的点P1，P2，P3，…，Pn，…，满足
OPn
=an
OA
+bn
OB
(n∈N*)，O为坐标原点，其中{an}、{bn}分别为等差数列和等比数列，P1是线段AB的中点，对于给定的公差不为零的an，都能找到唯一的一个bn，使得P1，P2，P3，…，Pn，…，都在一个指数函数
 
（写出函数的解析式）的图象上．
已知点集L={（x，y）|y=
m
•
n
}，其中
m
=（2x-b，1），
n
=（1，b+1），点列Pn（an，bn）（n∈N+）在L中，p1为L与y轴的交点，数列{an}是公差为1的等差数列．
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）若f（n）=
an，(n为奇数)
bn，(n为偶数)
，令Sn=f（1）+f（2）+f（3）+…+f（n），试写出Sn关于n的表达式；
（Ⅲ）若f（n）=
an，(n为奇数)
bn，(n为偶数)
，给定奇数m（m为常数，m∈N+，m＞2）．是否存在k∈N+，，使得
f（k+m）=2f（m），若存在，求出k的值；若不存在，请说明理由．
已知点集L={(x，y)|y=
m
•
n
}，其中
m
=（2x-b，1），
n
=（1，b+1），点列Pn（an，bn）在L中，P1为L与y轴的交点，等差数列{an}的公差为1，n∈N*．
（I）求数列{bn}的通项公式；
（Ⅱ）若f(n)=
an  n为正奇数
bn  n为正偶数
，令Sn=f（1）+f（2）+f（3）+…+f（n）；试写出Sn关于n的函数解析式；
已知点集L={(x，y)|y=
m
•
n
}，其中
m
=(2x-b，1)，
n
=(1，1+b)，又知点列Pn（an，bn）∈L，P1为L与y轴的交点．等差数列{an}的公差为1，n∈N*．
（Ⅰ）求Pn（an，bn）；
（Ⅱ）若f(n)=
an，n=2k-1
bn，n=2k
k∈N*，f(k+11)=2f(k)，求出k的值；
（Ⅲ）对于数列{bn}，设Sn是其前n项和，是否存在一个与n无关的常数M，使
Sn
S2n
=M，若存在，求出此常数M，若不存在，请说明理由．
已知点集L={(x，y)|y=
m
•
n
}，其中
m
=(2x-b，1)，
n
=(1，b+1)，点列Pn（an，bn）在L中，P1为L与y轴的交点，等差数列{an}的公差为1，n∈N+．
（1）求数列{an}，{bn}的通项公式；
（2）若f(n)=
an(n=2k-1)
bn(n=2k)
(k∈N+)，是否存在k∈N+使得f（k+11）=2f（k），若存在，求出k的值；若不存在，请说明理由．
（3）求证：
1
|P1P2|2
+
1
|P1P3|2
+…+
1
|P1Pn|2
＜
2
5
（n≥2，n∈N*）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网