题目内容
如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,且AE=AF.

(1)证明:B,D,H,E四点共圆;
(2)证明:CE平分∠DEF.
答案:
解析:
解析:
|
解:(Ⅰ)在△ABC中,因为∠B=60°, 所以∠BAC+∠BCA=120°. 因为AD,CE是角平分线, 所以∠HAC+∠HCA=60°, 故∠AHC=120°. 于是∠EHD=∠AHC=120°. 因为∠EBD+∠EHD=180°, 所以B,D,H,E四点共圆. (Ⅱ)连结BH,则BH为 由(Ⅰ)知B,D,H,E四点共圆, 所以 又 可得 所以CE平分
|

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目

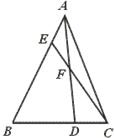 如图,已知△ABC中,AE:EB=1:3,BD:DC=2:1,AD与CE相交于F.求
如图,已知△ABC中,AE:EB=1:3,BD:DC=2:1,AD与CE相交于F.求 
 如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,
如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上, 如图,已知△ABC中,
如图,已知△ABC中, (2012•石家庄一模)如图,已知△ABC中,AB=
(2012•石家庄一模)如图,已知△ABC中,AB=