题目内容
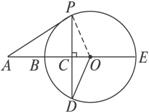
如图求证:AP是⊙O切线.
图
证明:连结OP,∵PD⊥BE,
∴∠OCD=90°.
∴∠ODC+∠COD=90°.
∵OD=OP,∴∠ODC=∠OPC.
∵∠COD=∠APC,
∴∠OPC+∠APC=90°.
∴∠APO=90°,即AP⊥PO.
∵P在⊙O上,∴AP是⊙O的切线.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
如图求证:AP是⊙O切线.

图
证明:连结OP,∵PD⊥BE,
∴∠OCD=90°.
∴∠ODC+∠COD=90°.
∵OD=OP,∴∠ODC=∠OPC.
∵∠COD=∠APC,
∴∠OPC+∠APC=90°.
∴∠APO=90°,即AP⊥PO.
∵P在⊙O上,∴AP是⊙O的切线.

 名校课堂系列答案
名校课堂系列答案