题目内容
设直线x=m与曲线f（x）=x2+1，g（x）=2lnx的图象分别交于点A，B，则|AB|的最小值为 ．
分析：当x=m时，|AB|=m2+1-2lnm，然后利用导数求出函数的最小值即可．
解答：解：当x=m时，|AB|=m2+1-2lnm，m＞0，
设f（m）=|AB|=m2+1-2lnm，
则f'（m）=2m-
=
，
由f'（m）＞0得m＞1，此时函数单调递增，
由f'（m）＜0得0＜m＜1，此时函数单调递减，
即当m=1时，函数取得极小值，同时也是最小值为f（1）=1+1-2ln1=2．
故答案为：2；
设f（m）=|AB|=m2+1-2lnm，
则f'（m）=2m-
| 2 |
| m |
| 2(m2-1) |
| m |
由f'（m）＞0得m＞1，此时函数单调递增，
由f'（m）＜0得0＜m＜1，此时函数单调递减，
即当m=1时，函数取得极小值，同时也是最小值为f（1）=1+1-2ln1=2．
故答案为：2；
点评：本题主要考查函数最值的求法，利用导数研究函数的极值是解决本题的关键．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
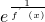-mx≥0恒成立，求实数m的最大值．
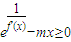恒成立，求实数m的最大值；
倍时，当x∈[1，e]时，若函数h（x）=f（x）-kf′（x）的最小值恰为g（x）的最小值，求实数k的值．