题目内容
已知α为锐角,并且有2tan(π-α)+3cos(
+β)+7=0,tan(π+α)+6sin(π+β)-1=0,则sinα=
.
| π |
| 2 |
3
| ||
| 10 |
3
| ||
| 10 |
分析:根据诱导公式把所给的两个条件进行化简整理,得到关于两个变量的二元一次方程组,解方程组求出tanα,最后根据同角三角函数关系求出sinα即可.
解答:解:∵2tan(π-α)+3cos(
+β)+7=0,tan(π+α)+6sin(π+β)-1=0
∴-2tanα-3sinβ+7=0…①
tanα-6sinβ-1=0…②
①×2+②得tanα=3,
即
=3
∵sin2α+cos2α=1
∵α为锐角,
∴sinα=
故答案为:
| π |
| 2 |
∴-2tanα-3sinβ+7=0…①
tanα-6sinβ-1=0…②
①×2+②得tanα=3,
即
| sinα |
| cosα |
∵sin2α+cos2α=1
∵α为锐角,
∴sinα=
3
| ||
| 10 |
故答案为:
3
| ||
| 10 |
点评:本题考查三角函数的化简求值,考查了诱导公式和同角三角函数关系,本题解题的关键是熟练应用三角函数的有关公式,本题属于基础题.

练习册系列答案
相关题目
 。
。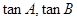 为方程
为方程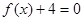 的两个实根,并且A,B为锐角,求m的取值范围;
的两个实根,并且A,B为锐角,求m的取值范围;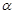 ,恒有
,恒有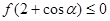 ,证明:
,证明: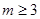 .
. +β)+7=0,tan(π+α)+6sin(π+β)-1=0,则sinα=________.
+β)+7=0,tan(π+α)+6sin(π+β)-1=0,则sinα=________. +β)+7=0,tan(π+α)+6sin(π+β)-1=0,则sinα= .
+β)+7=0,tan(π+α)+6sin(π+β)-1=0,则sinα= .