题目内容
如图1,矩形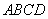 中,
中,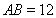 ,
,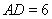 ,
, 、
、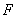 分别为
分别为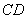 、
、 边上的点,且
边上的点,且 ,
,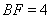 ,将
,将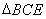 沿
沿 折起至
折起至 位置(如图2所示),连结
位置(如图2所示),连结 、
、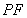 ,其中
,其中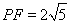 .
.
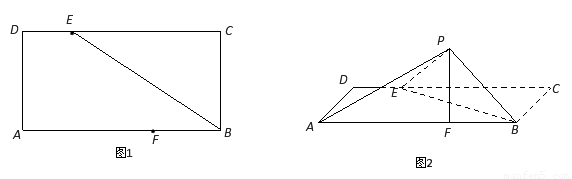
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)在线段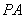 上是否存在点
上是否存在点 使得
使得 平面
平面 ?若存在,求出点
?若存在,求出点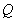 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(Ⅲ)求点 到平面
到平面 的距离.
的距离.
【答案】
(Ⅰ)答案详见解析;(Ⅱ)存在, ;(Ⅲ)
;(Ⅲ)  .
.
【解析】
试题分析:(Ⅰ)三角形 和三角形
和三角形 中,各边长度确定,故可利用勾股定理证明垂直关系
中,各边长度确定,故可利用勾股定理证明垂直关系
 ,进而由线面垂直的判定定理可证明
,进而由线面垂直的判定定理可证明 平面
平面 ;(Ⅱ)要使得
;(Ⅱ)要使得 平面
平面 ,只需
,只需 ,因为
,因为 ,故
,故 ;(Ⅲ)点到平面的距离,就是点到平面垂线段的长度,如果垂足位置不易确定,可考虑等体积转化,该题中点
;(Ⅲ)点到平面的距离,就是点到平面垂线段的长度,如果垂足位置不易确定,可考虑等体积转化,该题中点 到面
到面 的距离确定,故可利用
的距离确定,故可利用 求点
求点 到平面
到平面 的距离.
的距离.
试题解析:(Ⅰ)连结 ,由翻折不变性可知,
,由翻折不变性可知, ,
, ,在
,在 中,
中, ,所以
,所以 , 在图
, 在图 中,易得
中,易得 ,
,
在 中,
中, ,所以
,所以 ,又
,又 ,
, 平面
平面 ,
, 平面
平面 ,所以
,所以 平面
平面 .
.

(Ⅱ)当 为
为 的三等分点(靠近
的三等分点(靠近 )时,
)时, 平面
平面 .证明如下:
.证明如下:
因为 ,
, ,所以
,所以 , 又
, 又 平面
平面 ,
, 平面
平面 ,所以
,所以 平面
平面 .
.
(Ⅲ) 由(Ⅰ)知 平面
平面 ,所以
,所以 为三棱锥
为三棱锥 的高.
的高.
设点 到平面
到平面 的距离为
的距离为 ,由等体积法得
,由等体积法得 , 即
, 即 ,又
,又 ,
, , 所以
, 所以 , 即点
, 即点 到平面
到平面 的距离为
的距离为 .
.
考点:1、直线和平面垂直的判定定理;2、直线和平面平行的判定定理;3、点到平面的距离.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
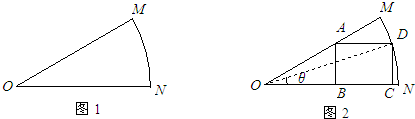 某车间为了制作某个零件,需从一块扇形的钢板余料(如图1)中按照图2的方式裁剪一块矩形钢板ABCD,其中顶点B、C在半径ON上,顶点A在半径OM上,顶点D在
某车间为了制作某个零件,需从一块扇形的钢板余料(如图1)中按照图2的方式裁剪一块矩形钢板ABCD,其中顶点B、C在半径ON上,顶点A在半径OM上,顶点D在

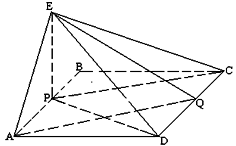 (1) 求证:
(1) 求证:  中,
中, ,
, ,
, 为
为 上的点,且
上的点,且 ,
, .(Ⅰ)求证:
.(Ⅰ)求证: 平面
平面 ;(Ⅱ)求证:
;(Ⅱ)求证: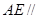 平面
平面 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥 的体积.
的体积.