题目内容
已知幂函数y=t(x)的图象过点(2,4),函数y=f(x)的图象可由y=t(x)的图象向左移动
个单位并向下移动
个单位得到.
(1)求函数t(x)和f(x)的解析式;
(2)若集合A={m∈R|当x∈[-2,2]时,函数g(x)=f(x)-mx具有单调性},集合B={m∈R|当0<x<
时,不等式f(x)+3<2x+m恒成立},求B∩(?RA)
| 1 |
| 2 |
| 9 |
| 4 |
(1)求函数t(x)和f(x)的解析式;
(2)若集合A={m∈R|当x∈[-2,2]时,函数g(x)=f(x)-mx具有单调性},集合B={m∈R|当0<x<
| 1 |
| 2 |
(1)设幂函数t(x)=xα,由其图象过点(2,4),所以,2α=4,解得α=2.
故t(x)=x2.
把y=t(x)的图象向左移动
个单位并向下移动
个单位,得f(x)=t(x+
)-
.
所以,f(x)=(x+
)2-
=x2+x+
-
=x2+x-2;
(2)由g(x)=f(x)-mx=x2+x-2-mx=x2-(m-1)x-2,
它的对称轴为x=
,
因为函数g(x)在区间[-2,2]上具有单调性,所以
≤-2或
≥2.
解得:m≤-3或m≥5.故A=(-∞,-3]∪[5,+∞).
再由f(x)+3<2x+m对x∈(0,
)恒成立,得:x2+x-2+3<2x+m对x∈(0,
)恒成立,
即m>x2-x+1对x∈(0,
)恒成立.
令h(x)=x2-x+1,对称轴为x=
,所以h(x)在(0,
)上为减函数,
所以h(x)<h(0)=1.所以m≥1.故B=[1,+∞).
所以CRA=(-3,5),
则B∩(?RA)=[1,+∞)∩(-3,5)=[1,5).
故t(x)=x2.
把y=t(x)的图象向左移动
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
所以,f(x)=(x+
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 4 |
| 9 |
| 4 |
(2)由g(x)=f(x)-mx=x2+x-2-mx=x2-(m-1)x-2,
它的对称轴为x=
| m-1 |
| 2 |
因为函数g(x)在区间[-2,2]上具有单调性,所以
| m-1 |
| 2 |
| m-1 |
| 2 |
解得:m≤-3或m≥5.故A=(-∞,-3]∪[5,+∞).
再由f(x)+3<2x+m对x∈(0,
| 1 |
| 2 |
| 1 |
| 2 |
即m>x2-x+1对x∈(0,
| 1 |
| 2 |
令h(x)=x2-x+1,对称轴为x=
| 1 |
| 2 |
| 1 |
| 2 |
所以h(x)<h(0)=1.所以m≥1.故B=[1,+∞).
所以CRA=(-3,5),
则B∩(?RA)=[1,+∞)∩(-3,5)=[1,5).

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 个单位并向下移动
个单位并向下移动 个单位得到.
个单位得到.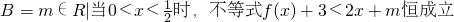 ,求B∩(?RA)
,求B∩(?RA) 个单位并向下移动
个单位并向下移动 个单位得到.
个单位得到. ,求B∩(∁RA)
,求B∩(∁RA)