Question

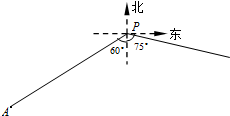如图，小岛A在港口P的南偏西60°方向，距离港口81n mile处．甲船从A出发，沿AP方向以9n mile/h的速度驶向港口，乙船从港口P出发，沿南偏东75°方向，以9

2

 n mile/h的速度驶离港口．现两船同时出发，
（1）出发后3h两船之间的距离是多少？
（2）出发后几小时乙船在甲船的正东方向？

Answer 1

分析：（1）设出发后3h甲船到达C点，乙船到达D点，则PC=54，PD=27

2

．在△PCD中，利用余弦定理求得CD即可得到出发后3h两船相距的距离；
（2）先设出发后xh乙船位于甲船的正东方向，此时甲船到达E点，乙船到达F点，结合题中条件在△PEF中利用正弦定理求得x即可．

解答：解：（1）设出发后3h甲船到达C点，乙船到达D点，则PC=54，PD=27

2

．
由题意，可知∠CPD=135°．
在△PCD中，CD²=PC²+PD²-2PC•PDcos∠CPD（2分）
=54²+（27

2

）²-2×54×27

2

×（-

2

2

）=27²×10=7290．
所以CD=27

10

．（3分）
所以出发后3h两船相距27

10

nmile．（4分）

（2）设出发后xh乙船位于甲船的正东方向，此时甲船到达E点，乙船到达F点，
则∠PEF=30°，∠PFE=15°，PE=81-9x，PF=9

2

x．
在△PEF中，

PE

sin∠PFE

=

PF

sin∠PEF

．即

81-9x

sin15°

=

9 2 x

sin30°

．（7分）
解得x=3

3

．（9分）
答：出发后3h两船相距27

10

nmile，出发后3

3

h乙船在甲船的正东方向．（10分）

点评：考查综合应用解三角形，进行逻辑推理能力和运算能力，解答关键是合理使用正弦定理和余弦定理．