题目内容
(18)某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.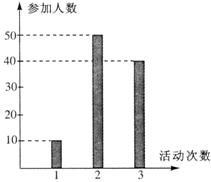
(Ⅰ)求合唱团学生参加活动的人均次数;
(Ⅱ)从合唱团中任选两名学生,求他们参加活动次数恰好相等的概率;
(Ⅲ)从合唱团中任选两名学生,用ξ表示这两人参加活动次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ.
解:由图可知,参加活动1次、2次和3次的学生人数分别为10、50和40.
(Ⅰ)该合唱团学生参加活动的人均次数为![]() =2.3.
=2.3.
(Ⅱ)从合唱团中任选两名学生,他们参加活动次数恰好相等的概率为
P0=![]() .
.
(Ⅲ)从合唱团中任选两名学生,记“这两人中一人参加1次活动,另一人参加2次活动”为事件A,“这两人中一人参加2次活动,另一人参加3次活动”为事件B,“这两人中一人参加1次活动,另一人参加3次活动”为事件C.易知
P(ξ=1)=P(A)+P(B)=![]() ;
;
P(ξ=2)=P(C)=![]()
又P(ξ=0)=P0=![]() .
.
ξ的分布列:
ξ | 0 | 1 | 2 |
P |
|
|
|
ξ的数学期望:Eξ=0×![]() +1×
+1×![]() +2×
+2×![]() =
=![]() .
.

练习册系列答案
相关题目
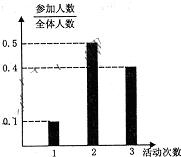 (理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
(理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示. 某中学号召学生在暑假期间至少参加一次社会公益活动(以下简称活动).该校文学社共有100名学生,他们参加活动的次数统计如图所示.则该文学社学生参加活动的人均次数为
某中学号召学生在暑假期间至少参加一次社会公益活动(以下简称活动).该校文学社共有100名学生,他们参加活动的次数统计如图所示.则该文学社学生参加活动的人均次数为