题目内容
给出下列不等式:
①a2+b2≥2(a+b-1)(a,b∈R);
②a5+b5≥a3b2+a2b3(a,b∈R);
③a>b>0,且 ,则ab>a2b2;
,则ab>a2b2;
④a,b∈R,且ab<0,则 ;
;
⑤a>b>0,m>0则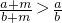 ;
;
⑥ .其中正确命题的个数是
.其中正确命题的个数是
- A.2
- B.3
- C.4
- D.5
D
分析:利用配方法能够判断①的正误;利用作差法能够判断②和⑤的正误;利用不等式性质能够判断③和④的正误;利用均值不等式能够判断⑥的正误.
解答:∵a2+b2-2(a+b-1)
=a2-2a+1+(b2-2b+1)
=(a-1)2+(b-1)2≥0,
∴a2+b2≥2(a+b-1)(a,b∈R),故①正确;
∵a5+b5-a3b2-a2b3
=a3(a2-b2)-b3(a2-b2)
=(a-b)2(a+b)(a2+ab+b2)≥0不成立,
∴a5+b5≥a3b2+a2b3(a,b∈R)不成立,故②不正确;
∵a>b>0,∴ab>b2,
∵ ,
,
∴ab>b2(a2+ )=
)= ,
,
∴ab>a2b2,故③成立;
∵(a+b)2≥0,
∴a2+b2≥-2ab,
∵ab<0,
∴ ,故④成立;
,故④成立;
∵a>b>0,m>0,
∴ -
-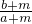 =
=
= <0,
<0,
所以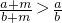 ,故⑤正确;
,故⑤正确;
当x>0时,y=x+
 =4,
=4,
当x<0时,y=x+ =-(-x-
=-(-x- )
) =-4,
=-4,
∴ ,故⑥正确.
,故⑥正确.
故选D.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,仔细解答,注意不等式的性质的灵活运用.
分析:利用配方法能够判断①的正误;利用作差法能够判断②和⑤的正误;利用不等式性质能够判断③和④的正误;利用均值不等式能够判断⑥的正误.
解答:∵a2+b2-2(a+b-1)
=a2-2a+1+(b2-2b+1)
=(a-1)2+(b-1)2≥0,
∴a2+b2≥2(a+b-1)(a,b∈R),故①正确;
∵a5+b5-a3b2-a2b3
=a3(a2-b2)-b3(a2-b2)
=(a-b)2(a+b)(a2+ab+b2)≥0不成立,
∴a5+b5≥a3b2+a2b3(a,b∈R)不成立,故②不正确;
∵a>b>0,∴ab>b2,
∵
 ,
,∴ab>b2(a2+
 )=
)= ,
,∴ab>a2b2,故③成立;
∵(a+b)2≥0,
∴a2+b2≥-2ab,
∵ab<0,
∴
 ,故④成立;
,故④成立;∵a>b>0,m>0,
∴
 -
-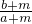 =
=
=
 <0,
<0,所以
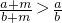 ,故⑤正确;
,故⑤正确;当x>0时,y=x+

 =4,
=4,当x<0时,y=x+
 =-(-x-
=-(-x- )
) =-4,
=-4,∴
 ,故⑥正确.
,故⑥正确.故选D.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,仔细解答,注意不等式的性质的灵活运用.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目