题目内容
在各项均为负数的数列{an}中,已知点 在函数
在函数 的图象上,且
的图象上,且 .求数列{an}的通项公式和前n项和Sn.
.求数列{an}的通项公式和前n项和Sn.
【答案】分析:根据点 在函数
在函数 的图象上,可得
的图象上,可得 ,从而数列{an}是公比为
,从而数列{an}是公比为 的等比数列,根据
的等比数列,根据 ,可得数列的通项,从而可求数列的和.
,可得数列的通项,从而可求数列的和.
解答:解:∵点 在函数
在函数 的图象上,
的图象上,
∴
∴数列{an}是公比为 的等比数列
的等比数列
∵
∴ ,∴
,∴ ,
,
由于数列{an}的各项均为负数,则
所以 ….(8分)
….(8分)
∴ .…(12分)
.…(12分)
点评:本题考查数列与函数的关系,考查数列的通项与求和,确定数列是等比数列是关键.
 在函数
在函数 的图象上,可得
的图象上,可得 ,从而数列{an}是公比为
,从而数列{an}是公比为 的等比数列,根据
的等比数列,根据 ,可得数列的通项,从而可求数列的和.
,可得数列的通项,从而可求数列的和.解答:解:∵点
 在函数
在函数 的图象上,
的图象上,∴

∴数列{an}是公比为
 的等比数列
的等比数列∵

∴
 ,∴
,∴ ,
,由于数列{an}的各项均为负数,则

所以
 ….(8分)
….(8分)∴
 .…(12分)
.…(12分)点评:本题考查数列与函数的关系,考查数列的通项与求和,确定数列是等比数列是关键.

练习册系列答案
相关题目
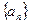 中,已知点
中,已知点 在
在 函数
函数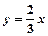 的图像上,且
的图像上,且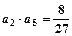 .
.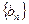 的前
的前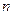 项和为
项和为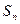 ,且
,且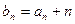 ,求
,求