题目内容
【题目】近日,某地普降暴雨,当地一大型提坝发生了渗水现象,当发现时已有![]() 的坝面渗水,经测算,坝而每平方米发生渗水现象的直接经济损失约为
的坝面渗水,经测算,坝而每平方米发生渗水现象的直接经济损失约为![]() 元,且渗水面积以每天
元,且渗水面积以每天![]() 的速度扩散.当地有关部门在发现的同时立即组织人员抢修渗水坝面,假定每位抢修人员平均每天可抢修渗水面积
的速度扩散.当地有关部门在发现的同时立即组织人员抢修渗水坝面,假定每位抢修人员平均每天可抢修渗水面积![]() ,该部门需支出服装补贴费为每人
,该部门需支出服装补贴费为每人![]() 元,劳务费及耗材费为每人每天
元,劳务费及耗材费为每人每天![]() 元.若安排
元.若安排![]() 名人员参与抢修,需要
名人员参与抢修,需要![]() 天完成抢修工作.
天完成抢修工作.
![]() 写出
写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 应安排多少名人员参与抢修,才能使总损失最小.(总损失=因渗水造成的直接损失+部门的各项支出费用)
应安排多少名人员参与抢修,才能使总损失最小.(总损失=因渗水造成的直接损失+部门的各项支出费用)
【答案】(1)![]() (2)应安排
(2)应安排![]() 名民工参与抢修,才能使总损失最小
名民工参与抢修,才能使总损失最小
【解析】
(1)由题意得要抢修完成必须使得抢修的面积等于渗水的面积,即可得![]() ,所以
,所以![]() ;
;
(2)损失包=渗水直接经济损失+抢修服装补贴费+劳务费耗材费,即可得到函数解析式,再利用基本不等式,即可得到结果.
![]() 由题意,可得
由题意,可得![]() ,所以
,所以![]() .
.
![]() 设总损失为
设总损失为![]() 元,则
元,则![]()
![]()
![]()
当且仅当![]() ,即
,即![]() 时,等号成立,
时,等号成立,
所以应安排![]() 名民工参与抢修,才能使总损失最小.
名民工参与抢修,才能使总损失最小.

 智慧小复习系列答案
智慧小复习系列答案【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:
分组 | 频数 | 频率 |
|
|
|
| 24 |
|
| 4 | 0.1 |
| 2 | 0.05 |
合计 |
| 1 |
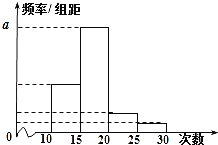
(1)求出表中![]() ,
,![]() 及图中
及图中![]() 的值;
的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间![]() 内的人数;
内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间![]() 内的概率.
内的概率.
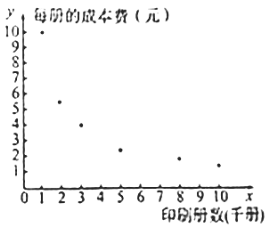
【题目】对某种书籍每册的成本费![]() (元)与印刷册数
(元)与印刷册数![]() (千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
(千册)的数据作了初步处理,得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
4.83 | 4.22 | 0.3775 | 60.17 | 0.60 | -39.38 | 4.8 |
其中![]() ,
,![]() .
.
为了预测印刷![]() 千册时每册的成本费,建立了两个回归模型:
千册时每册的成本费,建立了两个回归模型:![]() ,
,![]() .
.
(1)根据散点图,你认为选择哪个模型预测更可靠?(只选出模型即可)
(2)根据所给数据和(1)中的模型选择,求![]() 关于
关于![]() 的回归方程,并预测印刷
的回归方程,并预测印刷![]() 千册时每册的成本费.
千册时每册的成本费.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: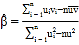 ,
,![]() .
.