题目内容
设函数f(x)=(1)求f(x)的单调区间和极值.
(2)是否存在实数a,使得关于x的不等式f(x)≥a的解集为(0,+∞)?若存在,求a的取值范围;若不存在,试说明理由.
本题主要考查函数的导数、单调性、极值,不等式等基础知识,考查综合利用数学知识分析问题、解决问题的能力.
解:(1)f′(x)=![]() .
.
故当x∈(0,1)时,f′(x)>0,
x∈(1,+∞)时,f′(x)<0.
所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
由此知f(x)在(0,+∞)上的极大值为f(1)=ln2,没有极小值.
(2)①当a≤0时,
由于f(x)=![]()
=![]() >0,
>0,
故关于x的不等式f(x)≥a的解集为(0,+∞).
②当a>0时,由f(x)=![]() +ln(1+
+ln(1+![]() )知f(2n)=
)知f(2n)=![]() +ln(1+
+ln(1+![]() ),其中n为正整数,且有ln(1+
),其中n为正整数,且有ln(1+![]() )<
)<![]()
![]() n>-log2(
n>-log2(![]() -1).
-1).
又n≥2时,![]() =
=![]() <
<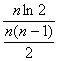 =
=![]() ,
,
且![]() <
<![]()
![]() n>
n>![]() +1.
+1.
取整数n0满足n0>-log2(![]() -1),n0>
-1),n0>![]() +1,且n0≥2,
+1,且n0≥2,
则f(![]() )=
)=![]() +ln(1+
+ln(1+![]() )<
)<![]() +
+![]() =a,
=a,
即当a>0时,关于x的不等式f(x)≥a的解集不是(0,+∞).
综合①②知,存在a,使得关于x的不等式f(x)≥a的解集为(0,+∞),且a的取值范围为(-∞,0].

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目