题目内容
例2.(1)对任意实数x,|x+1|+|x-2|>a恒成立,则a的取值范围是
(2)对任意实数x,|x-1|-|x+3|<a恒成立,则a的取值范围是
(-∞,3)
(-∞,3)
(2)对任意实数x,|x-1|-|x+3|<a恒成立,则a的取值范围是
(4,+∞)
(4,+∞)
分析:(1)利用绝对值的性质进行放缩,从而求解.
(2)同理可得|x-1|-|x+3|≤|x-1-(x+3)|,求出其最大值,即可求解.
(2)同理可得|x-1|-|x+3|≤|x-1-(x+3)|,求出其最大值,即可求解.
解答:解:(1)可由绝对值的几何意义或y=|x+1|+|x-2|的图象或者绝对值不等式的性质|x+1|+|x-2|=|x+1|+|2-x|≥|x+1+2-x|=3得|x+1|+|x-2|≥3,
∴a<3;
(2)与(1)同理可得|x-1|-|x+3|≤|x-1-(x+3)|=4,
∴a>4.
∴a<3;
(2)与(1)同理可得|x-1|-|x+3|≤|x-1-(x+3)|=4,
∴a>4.
点评:此题考查绝对值不等式的放缩问题及函数的恒成立问题,这类题目是高考的热点,难度不是很大,要注意不等号进行放缩的方向.

练习册系列答案
相关题目
 是抛物线
是抛物线

 的焦点,
的焦点, 是抛物线
是抛物线 上的
上的 个不同的点(
个不同的点(
 ).
). 时,试写出抛物线
时,试写出抛物线 上的三个定点
上的三个定点 、
、 、
、 的坐标,从而使得
的坐标,从而使得 ;
; 时,若
时,若 ,
, ;
; ,设
,设 ,
, 作抛物线
作抛物线 的垂线,垂足分别为
的垂线,垂足分别为 .
. ,分别过
,分别过 .
.

 时,抛物线
时,抛物线 分别过
分别过 作抛物线
作抛物线 .由抛物线定义得
.由抛物线定义得



 ,
, ,不妨取
,不妨取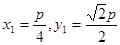 ;
;
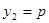 ;
;
 ;
;


 ,
,
 满足条件.
满足条件. ,分别过
,分别过

 又因为
又因为

 ;
;
 .
.

 ,
,

 .
.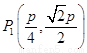 ,
, ,
, ,
, 是一个当
是一个当 时,该逆命题的一个反例.(反例不唯一)
时,该逆命题的一个反例.(反例不唯一) 及抛物线的定义得
及抛物线的定义得 ,即
,即 的纵坐标无关,所以只要将这
的纵坐标无关,所以只要将这 轴的上方,则它们的纵坐标都大于零,则
轴的上方,则它们的纵坐标都大于零,则




 ,所以
,所以 .
. 的一组
的一组 的纵坐标
的纵坐标 (
( )满足
)满足  ”,即:
”,即: ,且点
,且点 ,
, ,
, 与点
与点
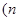 为偶数,
为偶数, 关于
关于