题目内容
设(1+x)2(1-3x)4=a0x6+a1x5+a2x4+a3x3+a4x2+a5x+a6,P={a0,a1,a2,a3,a4,a5,a6}.
(1)求满足Q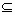 P的集合Q的个数;
P的集合Q的个数;
(2)求P含有5个元素的子集的个数n,若这n个子集中各子集元素之和分别记为R1,R2,R3,…,Rn,求R1+R2+R3+…+Rn.
答案:
解析:
解析:
|
(1)由二项式定理知a0,a1,a2,…a6互不相同. ∵Q (2)∵含有a0的5个元素的子集有 ∴R1+R2+…+Rn= |

练习册系列答案
相关题目
 P,∴Q的个数是:
P,∴Q的个数是: +…+
+…+ =27=128
=27=128 个,含有a1,a2,…,a6的5个元素的子集有
个,含有a1,a2,…,a6的5个元素的子集有 个,又含x=1,得:a0+a1+…+a6=64
个,又含x=1,得:a0+a1+…+a6=64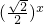 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是 ,1)
,1)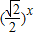 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( ) ,1)
,1)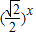 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( ) ,1)
,1)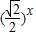 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( ) ,1)
,1)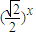 -1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( )
-1,若在区间(-2,6)内的关于x的方程f(x)-logga(x+2)=0(a>0且a≠1)恰有4个不同的实数根,则实数a的取值范围是( ) ,1)
,1)