Question

已知函数f（x）=2^x，数列{a_n}满足a₁=f（0），且．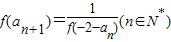
（1）证明数列{a_n}是等差数列，并求a₂₀₁₀的值；
（2）分别求出满足下列三个不等式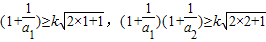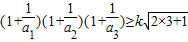：，的k的取值范围，并求出同时满足三个不等式的k的最大值；
（3）若不等式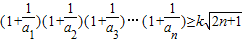对一切n∈N^*都成立，猜想k的最大值，并予以证明．

Answer 1

【答案】分析：（1）由已知条件化简得a_n+1=a_n+2，知a_n是等差数列，即a_n=2n-1，从而求得a₂₀₁₀=4019；
（2）先分别求出三个不等式中k的范围，当k同时满足三个不等式时，再求k的最大值．
（3）将已知条件变形，化成k≤F（n）恒成立问题，要求k的最大值即求F（n）的最小值，利用F（n）与F（n+1）的关系判断F（n）关于n的单调增函数，即F（n）的最小值就是F（1）．从而求得k的范围．
解答：解：（1）由，得f（a_n+1）•f（-2-a_n）=1（n∈N^*），
即，a_n+1=a_n+2，∴a_n是等差数列，∴a_n=2n-1，∴a₂₀₁₀=4019．（3分）

．∵，∴．（6分）
（3）．，
∴F（n+1）＞F（n），∴．（10分）
点评：此题考查等差数列的定义，及运用数列单调性来解决恒成立问题．