题目内容
10.在某次随机试验中,事件A发生的概率是sin2α(0<α<$\frac{π}{2}$),在3次这样的试验中,A恰好发生一次的概率的最大值为$\frac{4}{9}$.分析 根据n次独立重复实验中恰好发生k次的概率根式解答.
解答 解:由题意事件A发生的概率是sin2α(0<α<$\frac{π}{2}$),在3次这样的试验中,A恰好发生一次的概率${C}_{3}^{1}(1-si{n}^{2}α)^{2}si{n}^{2}α$=3cos4αsin2α,
设cos2α=x,则3cos4αsin2α=3t2(1-t)=-3t3+3t2=f(t),
令f'(t)=-9t2+6t=0,t=0(舍去)t=$\frac{2}{3}$∈(0,1),
所以f(t)的最大值为-3×$(\frac{2}{3})^{3}+3×(\frac{2}{3})^{2}$=$\frac{4}{9}$;
故答案为:$\frac{4}{9}$.
点评 本题主要考查n次独立重复实验中恰好发生k次的概率以及三角函数的最值求法.

练习册系列答案
相关题目
18.用反证法证明命题“若a+b=1,则a,b至少有一个不比1大时,”首先假设( )
| A. | a,b都小于等于1 | B. | a,b都大于1 | ||
| C. | a,b都大于等于1 | D. | a,b都小于1当a<0时 |
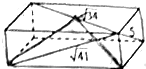 如图,已知长方体过一个顶点的三条面对角线的长分别为5,$\sqrt{34}$,$\sqrt{41}$,则其外接球(长方体的顶点均在球面上)的表面积是50π.
如图,已知长方体过一个顶点的三条面对角线的长分别为5,$\sqrt{34}$,$\sqrt{41}$,则其外接球(长方体的顶点均在球面上)的表面积是50π.