题目内容
已知奇函数f(x)=lg ,
,
(1)求a的值;
(2)判断函数f(x)在定义域上的单调性并证明.
解:(1)∵f(x)是奇函数∴f(x)+f(-x)=0,即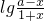
 =0 解得a=1
=0 解得a=1
故a的值为1
(2)由(1)知f(x)=lg ,定义域为(-1,1),
,定义域为(-1,1),
函数f(x)在定义域上单调递减,证明如下:
任取,x1,x2∈(-1,1)且x1<x2
f(x1)-f(x2)= -
- =
=
∵x1,x2∈(-1,1)且x1<x2
∴(1-x1+x2-x1x2)-(1+x1-x2-x1x2)=2(x2-x1)>0,
所以1-x1+x2-x1x2>1+x1-x2-x1x2,
因为1+x1-x2-x1x2=(1+x1)(1-x2)>0,
所以 ,从而
,从而 ,
,
即f(x1)>f(x2),
所以函数f(x)在定义域(-1,1)上单调递减.
分析:(1)根据奇函数的性质f(x)+f(-x)=0可求得a的值.
(2)先求得函数的定义域,再利用函数单调性的定义判断并证明函数f(x)在定义域上的单调性.
点评:本题考查了函数的单调性,本题需要用定义证明,化简时需要注意应先比较真数与1的大小,才能得到f(x1)与f(x2)的大小,计算量大,属中档题.
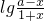
 =0 解得a=1
=0 解得a=1故a的值为1
(2)由(1)知f(x)=lg
 ,定义域为(-1,1),
,定义域为(-1,1),函数f(x)在定义域上单调递减,证明如下:
任取,x1,x2∈(-1,1)且x1<x2
f(x1)-f(x2)=
 -
- =
=
∵x1,x2∈(-1,1)且x1<x2
∴(1-x1+x2-x1x2)-(1+x1-x2-x1x2)=2(x2-x1)>0,
所以1-x1+x2-x1x2>1+x1-x2-x1x2,
因为1+x1-x2-x1x2=(1+x1)(1-x2)>0,
所以
 ,从而
,从而 ,
,即f(x1)>f(x2),
所以函数f(x)在定义域(-1,1)上单调递减.
分析:(1)根据奇函数的性质f(x)+f(-x)=0可求得a的值.
(2)先求得函数的定义域,再利用函数单调性的定义判断并证明函数f(x)在定义域上的单调性.
点评:本题考查了函数的单调性,本题需要用定义证明,化简时需要注意应先比较真数与1的大小,才能得到f(x1)与f(x2)的大小,计算量大,属中档题.

练习册系列答案
相关题目