题目内容
下列曲线的所有切线构成的集合中,存在无数对互相垂直的切线的曲线是( )A.f(x)=ex
B.f(x)=x3
C.f(x)=ln
D.f(x)=sin
【答案】分析:设出切点坐标,利用曲线在切点处的导数值是曲线的切线斜率,将存在无数对互相垂直的切线转化为f′(x1)•f′(x2)=-1有无数对x1,x2使之成立;对四个选项的函数判断是否符合.
解答:解:设切点的横坐标为x1,x2
则存在无数对互相垂直的切线,即f′(x1)•f′(x2)=-1有无数对x1,x2使之成立
对于A由f′(x)=ex>0,
所以不存在f′(x1)•f′(x2)=-1成立;
对于B由于f′(x)=3x2>0,
所以也不存在f′(x1)•f′(x2)=-1成立;
对于C由于f(x)=lnx的定义域为(0,+∞),
∴f′(x)= >0,
>0,
对于Df′(x)=cosx,
∴f′(x1)•f′(x2)=cosx1•cosx2,
当x1=2kπ,x2=(2k+1)π,k∈Z,
f′(x1)•f′(x2)=-1恒成立.
故选D
点评:本题考查导数的几何意义:曲线在切点处的导数值是曲线的切线斜率;等价转化的能力.
解答:解:设切点的横坐标为x1,x2
则存在无数对互相垂直的切线,即f′(x1)•f′(x2)=-1有无数对x1,x2使之成立
对于A由f′(x)=ex>0,
所以不存在f′(x1)•f′(x2)=-1成立;
对于B由于f′(x)=3x2>0,
所以也不存在f′(x1)•f′(x2)=-1成立;
对于C由于f(x)=lnx的定义域为(0,+∞),
∴f′(x)=
 >0,
>0,对于Df′(x)=cosx,
∴f′(x1)•f′(x2)=cosx1•cosx2,
当x1=2kπ,x2=(2k+1)π,k∈Z,
f′(x1)•f′(x2)=-1恒成立.
故选D
点评:本题考查导数的几何意义:曲线在切点处的导数值是曲线的切线斜率;等价转化的能力.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
下列曲线的所有切线构成的集合中,存在无数对互相垂直的切线的曲线是( )
| A、f(x)=ex | B、f(x)=x3 | C、f(x)=lnx | D、f(x)=sinx |
 ②
② ③
③ ④
④
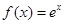 ②
② ③
③ ④
④