题目内容
已知函数f (x)=ax2+bx+ 与直线y=x相切于点A(1,1),若对任意x∈[1,9],不等式f (x-t)≤x恒成立,则所有满足条件的实数t的值为 .
与直线y=x相切于点A(1,1),若对任意x∈[1,9],不等式f (x-t)≤x恒成立,则所有满足条件的实数t的值为 .
【答案】分析:对f(x)进行求导,根据它与直线y=x相切于点A(1,1),可得f′(1)=0,可得把点A代入得到方程,求出a,b,求出f(x)的解析式,根据题意对任意x∈[1,9],不等式f (x-t)≤x恒成立,根据根与系数的关系进行求解;
解答:解:∵已知函数f (x)=ax2+bx+ 与直线y=x相切于点A(1,1),
与直线y=x相切于点A(1,1),
f′(x)=2ax+b,
∴f′(1)=1,可得2a+b=1①,又f(x)过点A(1,1)可得a+b+ =1②,
=1②,
联立方程①②可得a= ,b=
,b= ,
,
f(x)= x2+
x2+ x+
x+ ,
,
∵对任意x∈[1,9],不等式f (x-t)≤x恒成立,
可得f(x-t)= (x-t+1)2≤x,
(x-t+1)2≤x,
化简可得,x2-2x(t-1)+(t-1)2-4x≤0,在[1,9]上恒成立,
令g(x)=x2-2x(t+1)+(t-1)2≤0,在[1,9]上恒成立,
∴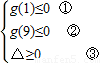 ,
,
解①可得0≤t≤4,
解②可得4≤t≤14,
解③可得t≥4
综上可得:t=4,
故答案为4
点评:考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值.掌握不等式恒成立时所取的条件;
解答:解:∵已知函数f (x)=ax2+bx+
 与直线y=x相切于点A(1,1),
与直线y=x相切于点A(1,1),f′(x)=2ax+b,
∴f′(1)=1,可得2a+b=1①,又f(x)过点A(1,1)可得a+b+
 =1②,
=1②,联立方程①②可得a=
 ,b=
,b= ,
,f(x)=
 x2+
x2+ x+
x+ ,
,∵对任意x∈[1,9],不等式f (x-t)≤x恒成立,
可得f(x-t)=
 (x-t+1)2≤x,
(x-t+1)2≤x,化简可得,x2-2x(t-1)+(t-1)2-4x≤0,在[1,9]上恒成立,
令g(x)=x2-2x(t+1)+(t-1)2≤0,在[1,9]上恒成立,
∴
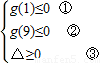 ,
,解①可得0≤t≤4,
解②可得4≤t≤14,
解③可得t≥4
综上可得:t=4,
故答案为4
点评:考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值.掌握不等式恒成立时所取的条件;

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|