题目内容
在数列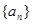 中,
中,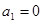 ,且对任意k
,且对任意k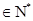 ,
,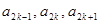 成等差数列,其公差为
成等差数列,其公差为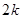 .
.
⑴求 ;
;
⑵求数列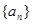 的通项公式;
的通项公式;
⑶记. , 证明:
, 证明: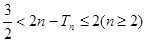 .
.
【答案】
解:⑴证明:由题设可知, ,
, ,
, ,……3分
,……3分
⑵解:由题设可得
所以

 .
.
由 ,得
,得 ,从而
,从而 .
.
所以数列 的通项公式为
的通项公式为 或写为
或写为 ,
, 。
。  ……7分
……7分
⑶证明:由⑵可知当 为偶数时,
为偶数时, ;
;
当 为奇数时,
为奇数时, .……8分
.……8分
易知 时,
时, . 不等式成立。
……9分
. 不等式成立。
……9分
又当 为偶数且
为偶数且 时,
时,





 ……11分
……11分
 ,从而
,从而 ,不等式也成立。……12分
,不等式也成立。……12分
当 为奇数时,
为奇数时,
=
=
=

从而 ,
,
综上, . ……14分
. ……14分
【解析】略

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
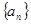 中,
中,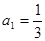 ,且对任意
,且对任意 都有
都有 成立,令
成立,令 (1)求数列
(1)求数列 的通项公式;(2)求数列
的通项公式;(2)求数列 的前n项和
的前n项和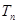 。
。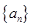 中,
中, ,且对任意
,且对任意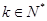 .
. ,
, ,
,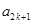 成等差数列,其公差为
成等差数列,其公差为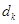 。
。 ,证明
,证明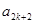 成等比数列(
成等比数列(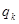 。
证明:对任意
。
证明:对任意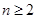 ,
, ,有
,有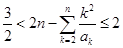
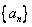 中,
中, ,且对任意
,且对任意 .
.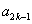 ,
,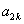 ,
, 成等差数列,其公差为
成等差数列,其公差为 。
。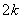 ,证明
,证明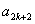 成等比数列(
成等比数列( 。
。 中,
中, ,且对任意
,且对任意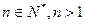 都有
都有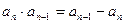 成立,令
成立,令 (1)求数列
(1)求数列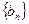 的通项公式;(2)求数列
的通项公式;(2)求数列 的前n项和
的前n项和 。
。