题目内容
(本小题满分12分)
如图4,三棱柱![]() 中,侧面
中,侧面![]()
![]() 底面
底面![]() ,
,![]() ,且
,且![]() ,O为
,O为![]() 中点.
中点.
(Ⅰ)在![]() 上确定一点
上确定一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
 (Ⅱ)求二面角
(Ⅱ)求二面角![]() 的大小.
的大小.
(本小题满分12分)
解:(Ⅰ)![]() 为
为![]() 中点. 2分
中点. 2分
证法一:取![]() 中点
中点![]() ,连接
,连接![]() . 3分
. 3分
所以可得![]() ,所以面
,所以面![]() 面
面![]() . 5分
. 5分
所以![]() 平面
平面![]() . 6分
. 6分
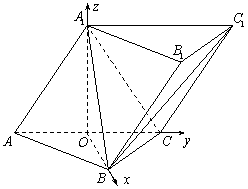 证法二:因为
证法二:因为![]() ,且O为
,且O为![]()
的中点,所以![]() .又由题意可知,
.又由题意可知,
平面![]() 平面
平面![]() ,交线为
,交线为![]() ,
,
且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
以O为原点,![]() 所在直线分别
所在直线分别
为x,y,z轴建立空间直角坐标系.…………1分
由题意可知,![]() 又
又![]()
![]()
所以得:![]()
则有:![]() . 2分
. 2分
设平面![]() 的一个法向量为
的一个法向量为![]() ,则有
,则有
![]() ,令
,令![]() ,得
,得![]()
所以![]() . 4分
. 4分
设![]() 即
即![]() ,得
,得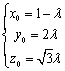
所以![]() 得
得![]() 由已知
由已知![]() 平面
平面![]() ,
,
得![]() , 即
, 即![]() 得
得![]() .
.
即存在这样的点![]() ,
,![]() 为
为![]() 的中点. 6分
的中点. 6分
(Ⅱ)由法二,已知![]() ,设面
,设面![]() 的法向量为
的法向量为
|
|
|
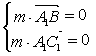
|
|
|
|
|
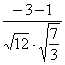 =
=由图可得二面角![]() 的大小为
的大小为![]() . 12分
. 12分

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目