题目内容
定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足f(x0)=
,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.如y=x4是[-1,1]上的平均值函数,0就是它的均值点.现有函数f(x)=-x2+mx+1是区间[-1,1]上的平均值函数,则实数m的取值范围是______.
| f(b)-f(a) |
| b-a |
)∵函数f(x)=-x2+mx+1是区间[-1,1]上的平均值函数,
∴关于x的方程-x2+mx+1=
在(-1,1)内有实数根.
由-x2+mx+1=
?x2-mx+m-1=0,解得x=m-1,x=1.
又1∉(-1,1)
∴x=m-1必为均值点,即-1<m-1<1?0<m<2.
∴所求实数m的取值范围是0<m<2.
故答案为:0<m<2.
∴关于x的方程-x2+mx+1=
| f(1)-f(-1) |
| 1-(-1) |
由-x2+mx+1=
| f(1)-f(-1) |
| 1-(-1) |
又1∉(-1,1)
∴x=m-1必为均值点,即-1<m-1<1?0<m<2.
∴所求实数m的取值范围是0<m<2.
故答案为:0<m<2.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
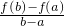 ,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.如y=x4是[-1,1]上的平均值函数,0就是它的均值点.
,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.如y=x4是[-1,1]上的平均值函数,0就是它的均值点.