题目内容
给出下列四个命题:
①
② ,使得
,使得 成立;
成立;
③ 为长方形,
为长方形, ,
, ,
,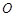 为
为 的中点,在长方形
的中点,在长方形 内随机取一 点,取得的点到
内随机取一 点,取得的点到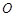 距离大小1的概率为
距离大小1的概率为 ;
;
④在 中,若
中,若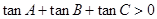 ,则
,则 是锐角三角形,
是锐角三角形,
其中正确命题的序号是
①②④
解析试题分析:①设f(x)= ,则设f′(x)=
,则设f′(x)= ,当x≥1时,f′(x)=
,当x≥1时,f′(x)= ≥0,
≥0,
故f(x)= ,在[1,+∞)上是增函数,∴当x≥1时,f(x)≥f(1),即
,在[1,+∞)上是增函数,∴当x≥1时,f(x)≥f(1),即 ≥0,∴
≥0,∴ 同理,当x<1时,也有
同理,当x<1时,也有 .∴
.∴ 成立.①是正确命题;②将
成立.①是正确命题;②将 =1代入:
=1代入: <0,将
<0,将 =2代入
=2代入 >0,故
>0,故 ,使得
,使得 成立.②是正确命题;③已知如图所示:长方形面积为2,以O为圆心,1为半径作圆,在矩形内部的部分(半圆)面积为
成立.②是正确命题;③已知如图所示:长方形面积为2,以O为圆心,1为半径作圆,在矩形内部的部分(半圆)面积为 ,因此取到的点到O的距离大于1的概率P=
,因此取到的点到O的距离大于1的概率P= .③是不正确命题;④∵tanA+tanB=tan(A+B)(1-tanAtanB)∴tanA+tanB+tanC=tan(A+B)(1-tanAtanB)+tanC=tanAtanBtanC>0,∴A,B,C是△ABC的内角,故内角都是锐角,④是正确命题.
.③是不正确命题;④∵tanA+tanB=tan(A+B)(1-tanAtanB)∴tanA+tanB+tanC=tan(A+B)(1-tanAtanB)+tanC=tanAtanBtanC>0,∴A,B,C是△ABC的内角,故内角都是锐角,④是正确命题.
其中正确命题的序号是 ①②④.
考点:本题考查了命题真假的判断
点评:本题以命题真假为背景,主要考查了几何概型、三角形的形状判断、导数等知识

练习册系列答案
相关题目
 的图象向右平移
的图象向右平移 个单位,得到
个单位,得到 的图象;
的图象; 的图象在x=1处的切线平行于直线y=x,则
的图象在x=1处的切线平行于直线y=x,则 是f(x)的单调递增区间;
是f(x)的单调递增区间; 的值为2;
的值为2; ,则
,则 与
与 的夹角为钝角;
的夹角为钝角; ,则不等式
,则不等式 成立的概率是
成立的概率是 ;
; 的最小值为2.
的最小值为2. ,都有
,都有
 (除数
(除数 ),则称P是一个数域.例如有理数集Q是数域;数集
),则称P是一个数域.例如有理数集Q是数域;数集 也是数域.有下列命题:
也是数域.有下列命题: ,则数集M必为数域;
,则数集M必为数域; ;
; 是奇函数;
是奇函数; 的一个对称中心是(-
的一个对称中心是(- ;
; 的图象可由
的图象可由 的图象向右平移
的图象向右平移 个单位得到。
个单位得到。 ”的 条件。
”的 条件。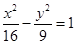 与椭圆
与椭圆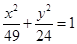 有相同的焦点;
有相同的焦点; 、
、 为两个定点,
为两个定点,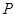 为动点,且
为动点,且 ,其中常数
,其中常数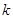 为正实数,则动点
为正实数,则动点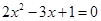 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;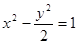 的右焦点
的右焦点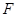 作直线
作直线 交双曲线于
交双曲线于 两点,若
两点,若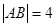 ,则这样的直线
,则这样的直线
 的图像一定过定点
的图像一定过定点 ;
; 的定义域是
的定义域是 ,则函数
,则函数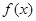 的定义域为
的定义域为 ;
; ,且
,且 =8,则
=8,则 =-8;
=-8; 且
且 ,则实数
,则实数 .
. 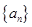 中,若
中,若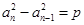 ,(n≥2,n∈N*,p为常数),则称
,(n≥2,n∈N*,p为常数),则称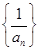 是等差数列;②
是等差数列;②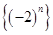 是“等方差数列”;
是“等方差数列”;