题目内容
已知函数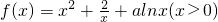 在[1,+∞)上单调递增,则a的取值范围是________.
在[1,+∞)上单调递增,则a的取值范围是________.
a≥0
分析:求导函数可得 (x>0),函数
(x>0),函数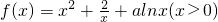 在[1,+∞)上单调递增,转化为
在[1,+∞)上单调递增,转化为 ≥0在[1,+∞)上恒成立,分离参数可得a≥-2x2+
≥0在[1,+∞)上恒成立,分离参数可得a≥-2x2+ ,求出右边函数的最大值,即可得到结论.
,求出右边函数的最大值,即可得到结论.
解答:求导函数可得 (x>0)
(x>0)
∵函数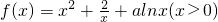 在[1,+∞)上单调递增,
在[1,+∞)上单调递增,
∴ ≥0在[1,+∞)上恒成立
≥0在[1,+∞)上恒成立
∴a≥-2x2+
令g(x)=-2x2+ ,则g′(x)=-4x-
,则g′(x)=-4x- ≤0在[1,+∞)上恒成立
≤0在[1,+∞)上恒成立
∴函数g(x)=-2x2+ 在[1,+∞)上单调减
在[1,+∞)上单调减
∴x=1时,函数g(x)=-2x2+ 取得最大值0
取得最大值0
∴a≥0
故答案为:a≥0
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,求函数的最值是关键.
分析:求导函数可得
 (x>0),函数
(x>0),函数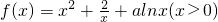 在[1,+∞)上单调递增,转化为
在[1,+∞)上单调递增,转化为 ≥0在[1,+∞)上恒成立,分离参数可得a≥-2x2+
≥0在[1,+∞)上恒成立,分离参数可得a≥-2x2+ ,求出右边函数的最大值,即可得到结论.
,求出右边函数的最大值,即可得到结论.解答:求导函数可得
 (x>0)
(x>0)∵函数
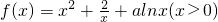 在[1,+∞)上单调递增,
在[1,+∞)上单调递增,∴
 ≥0在[1,+∞)上恒成立
≥0在[1,+∞)上恒成立∴a≥-2x2+

令g(x)=-2x2+
 ,则g′(x)=-4x-
,则g′(x)=-4x- ≤0在[1,+∞)上恒成立
≤0在[1,+∞)上恒成立∴函数g(x)=-2x2+
 在[1,+∞)上单调减
在[1,+∞)上单调减∴x=1时,函数g(x)=-2x2+
 取得最大值0
取得最大值0∴a≥0
故答案为:a≥0
点评:本题考查导数知识的运用,考查函数的单调性,考查恒成立问题,求函数的最值是关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
 在[-1,+ ∞)上是减函数,则a的取值范围是
.
在[-1,+ ∞)上是减函数,则a的取值范围是
. 在[1,+∞)上为增函数,且
在[1,+∞)上为增函数,且 ,
, ,
, ∈R.
∈R. 在[1,+∞)上为单调函数,求m的取值范围;
在[1,+∞)上为单调函数,求m的取值范围; ,若在[1,e]上至少存在一个
,若在[1,e]上至少存在一个 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围. 在[1,+∞)上为增函数,且
在[1,+∞)上为增函数,且 ,
, 的值;
的值; 在[1,+∞)上为单调函数,求实数
在[1,+∞)上为单调函数,求实数 的取值范围;
的取值范围; 上至少存在一个
上至少存在一个 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围. 在[1,2]上的值恒为正,则a的取值范围是( )
在[1,2]上的值恒为正,则a的取值范围是( ) B.
B. C.
C. D.
D.
 在[1,2]上的值恒为正,则a的取值范围是( )
在[1,2]上的值恒为正,则a的取值范围是( ) B.
B. C.
C. D.
D.