Question

（本题12分）已知集合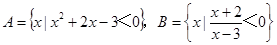
（Ⅰ）在区间（－4,4）上任取一个实数x，求“x∈A∩B”的概率；
（Ⅱ）设（a,b）为有序实数对，其中a是从集合A中任取的一个整数，b是从集合B中任取的一个整数，求“b－a∈A∪B”的概率.

Answer 1

（Ⅰ）（Ⅱ）

解析试题分析：（Ⅰ）由已知,设事件“x∈A∩B”的概率为，则
（Ⅱ）
基本事件共12个，（－2,－1）,（－2,0），（－2,1），（－2,2），（－1,－1），（－1,0），（－1,1），（－1,2），（0, －1），（0,0），（0,1），（0,2）
设事件E为“b－a∈A∪B”，则事件E中包含9个基本事件.

考点：本题主要考查集合的运算，简单不等式解法，几何概型、古典概型概率的计算。
点评：综合题，古典概型概率的计算，公式明确，关键是计算基本事件数要准确，可借助于“树图法”“坐标法”。