题目内容
在△ABC中,若 ,则△ABC的形状是
,则△ABC的形状是
- A.直角三角形
- B.等腰三角形
- C.等腰直角三角形
- D.等腰三角形或直角三角形
D
分析:当A不等于B时,根据正弦定理化简已知等式的右边,然后和差化积后,再利用同角三角函数间的基本关系弦化切后,两边同时除以tan ,得到tan
,得到tan 的值,由A和B都为三角形的内角,得到A+B为直角,从而得到三角形为直角三角形;若A=B,根据“等角对等边”得到a=b,显然已知等式成立,此时三角形为等腰三角形,综上,三角形ABC的形状为直角三角形或等腰三角形.
的值,由A和B都为三角形的内角,得到A+B为直角,从而得到三角形为直角三角形;若A=B,根据“等角对等边”得到a=b,显然已知等式成立,此时三角形为等腰三角形,综上,三角形ABC的形状为直角三角形或等腰三角形.
解答:当A≠B时,根据正弦定理得:
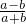 =
= =
= =
= ,
,
又 ,
,
∴tan =1,又A和B都为三角形的内角,
=1,又A和B都为三角形的内角,
∴ =
= ,
,
解得A+B= ,即C=
,即C= ,
,
则△ABC为直角三角形;
当A=B时,a=b, 显然成立,
显然成立,
则△ABC为等腰三角形,
综上,△ABC为等腰三角形或直角三角形.
故选D
点评:此题考查了三角形形状的判断,涉及的知识有正弦定理,和差化积公式,同角三角函数间的基本关系,等腰三角形的判定的以及特殊角的三角函数值,根据A与B相等与不相等两种情况分类讨论,进而得出三角形的形状.由三角函数的恒等变形化简已知的等式得到tan 的值是解本题的关键.
的值是解本题的关键.
分析:当A不等于B时,根据正弦定理化简已知等式的右边,然后和差化积后,再利用同角三角函数间的基本关系弦化切后,两边同时除以tan
 ,得到tan
,得到tan 的值,由A和B都为三角形的内角,得到A+B为直角,从而得到三角形为直角三角形;若A=B,根据“等角对等边”得到a=b,显然已知等式成立,此时三角形为等腰三角形,综上,三角形ABC的形状为直角三角形或等腰三角形.
的值,由A和B都为三角形的内角,得到A+B为直角,从而得到三角形为直角三角形;若A=B,根据“等角对等边”得到a=b,显然已知等式成立,此时三角形为等腰三角形,综上,三角形ABC的形状为直角三角形或等腰三角形.解答:当A≠B时,根据正弦定理得:
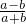 =
= =
= =
= ,
,又
 ,
,∴tan
 =1,又A和B都为三角形的内角,
=1,又A和B都为三角形的内角,∴
 =
= ,
,解得A+B=
 ,即C=
,即C= ,
,则△ABC为直角三角形;
当A=B时,a=b,
 显然成立,
显然成立,则△ABC为等腰三角形,
综上,△ABC为等腰三角形或直角三角形.
故选D
点评:此题考查了三角形形状的判断,涉及的知识有正弦定理,和差化积公式,同角三角函数间的基本关系,等腰三角形的判定的以及特殊角的三角函数值,根据A与B相等与不相等两种情况分类讨论,进而得出三角形的形状.由三角函数的恒等变形化简已知的等式得到tan
 的值是解本题的关键.
的值是解本题的关键. 
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 ,则B的值为( )
,则B的值为( )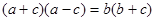 ,则∠A=( )
,则∠A=( ) B.
B. C.
C.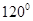 D.
D.
 ,则∠A=
,则∠A= 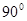 B.
B.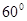 C.
C. D.
D.
 ,
, ,若
,若 ,
, ,则
,则 ()
()  A.
A. B.
B.
 D.
D.
 ,则其面积等于( )
,则其面积等于( ) B.
B. C.1
D.2
C.1
D.2