题目内容
已知x+2y=1，x∈R+，y∈R+，则x2y的最大值为 ．
【答案】分析：法一：由x+2y=1，可得x=1-2y，结合x＞0，y＞0可得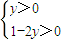
，而x2y=（1-2y）2y=
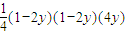，利用基本不等式可求函数的最大值
法二：由x+2y=1，可得x=1-2y，解x＞0，y＞0可得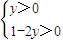
，而x2y=（1-2y）2y=4y3-4y2+y，构造函数f（y）=4y3-4y2+y（
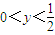），利用导数判断函数的单调性，进而可求函数的最大值
解答：解：法一：由x+2y=1，可得x=1-2y
∵x＞0，y＞0
∴
∴
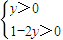
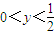
∴x2y=（1-2y）2y=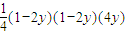
=
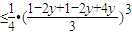
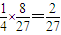
当且仅当1-2y=4y即y=
，x=
时取等号
则x2y的最大值为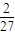
故答案为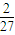
法二：由x+2y=1，可得x=1-2y
∴x2y=（1-2y）2y=4y3-4y2+y
∵x＞0，y＞0
∴
∴
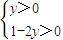
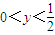
令f（y）=4y3-4y2+y（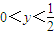
），则f′（y）=12y2-8y+1
∵
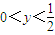
令f′（y）＜0恒可得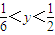
令f′（y）≥0可得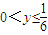
∴函数f（y）=4y3-4y2+y在（
，
）单调递减，在（0，
]上单调递增
∴当y=
时取得最大值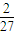
故答案为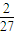
点评：本题主要考查了函数的最大值的求解，法一中主要利用了基本不等式abc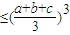
，法二是解答一般函数求解最值的常用方法
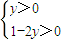，而x2y=（1-2y）2y=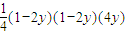，利用基本不等式可求函数的最大值法二：由x+2y=1，可得x=1-2y，解x＞0，y＞0可得
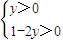，而x2y=（1-2y）2y=4y3-4y2+y，构造函数f（y）=4y3-4y2+y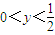（），利用导数判断函数的单调性，进而可求函数的最大值解答：解：法一：由x+2y=1，可得x=1-2y
∵x＞0，y＞0
∴
∴
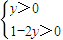
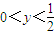
∴x2y=（1-2y）2y=
=
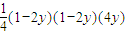
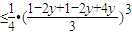
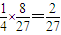
当且仅当1-2y=4y即y=
，x=时取等号则x2y的最大值为
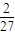
故答案为
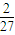
法二：由x+2y=1，可得x=1-2y
∴x2y=（1-2y）2y=4y3-4y2+y
∵x＞0，y＞0
∴
∴
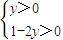
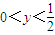
令f（y）=4y3-4y2+y（
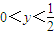），则f′（y）=12y2-8y+1∵
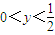
令f′（y）＜0恒可得
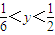
令f′（y）≥0可得
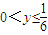
∴函数f（y）=4y3-4y2+y在（
，）单调递减，在（0，]上单调递增∴当y=
时取得最大值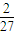故答案为
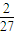
点评：本题主要考查了函数的最大值的求解，法一中主要利用了基本不等式abc
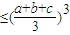，法二是解答一般函数求解最值的常用方法 
练习册系列答案
相关题目