题目内容
20.如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
(Ⅰ)求BF的长;
(Ⅱ)求点C到平面AEC1F的距离.

20.本小题主要考查线面关系和空间距离的求法等基础知识,同时考查空间想象能力和推理运算能力.
解法1:(Ⅰ)过E作EH//BC交CC1于H,则CH=BE=1,EH//AD,且EH=AD.

又∵AF∥EC1,∴∠FAD=∠C1EH.
∴Rt△ADF≌Rt△EHC1. ∴DF=C1H=2.
![]()
(Ⅱ)延长C1E与CB交于G,连AG,
则平面AEC1F与平面ABCD相交于AG.
过C作CM⊥AG,垂足为M,连C1M,
由三垂线定理可知AG⊥C1M.由于AG⊥面C1MC,且
AG![]() 面AEC1F,所以平面AEC1F⊥面C1MC.在Rt△C1CM中,作CQ⊥MC1,垂足为Q,则CQ的长即为C到平面AEC1F的距离.
面AEC1F,所以平面AEC1F⊥面C1MC.在Rt△C1CM中,作CQ⊥MC1,垂足为Q,则CQ的长即为C到平面AEC1F的距离.

解法2:(I)建立如图所示的空间直角坐标系,则D(0,0,0),B(2,4,0),A(2,0,0),
C(0,4,0),E(2,4,1),C1(0,4,3).设F(0,0,z).

∵AEC1F为平行四边形,

(II)设![]() 为平面AEC1F的法向量,
为平面AEC1F的法向量,
![]()


![]() 的夹角为a,则
的夹角为a,则

∴C到平面AEC1F的距离为
![]()

练习册系列答案
相关题目
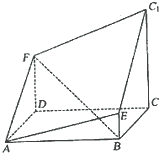 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1. 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1. 已知:如图所示的多面体是由底面为ABCD的长方体被截面AEGF所截得的,其中AB=4,BC=2,CG=3,BE=1,
已知:如图所示的多面体是由底面为ABCD的长方体被截面AEGF所截得的,其中AB=4,BC=2,CG=3,BE=1,
