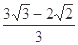题目内容
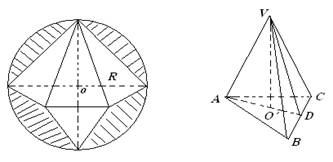
将半径为R的圆面剪切去如图中的阴影部分,沿图所画的线折成一个正三棱锥,这个正三棱锥的侧面与底面所成的二面角的余弦值是( )
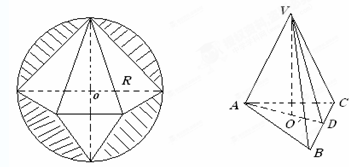

分析:作VO′⊥平面ABC,垂足为O′作AD⊥BC,连接VD,则O′在AD上,∠VDO′为正三棱锥的侧面与底面所成的二面角,求得AB,VC的关系,即可求得结论.
解答:解:由题意,作VO′⊥平面ABC,垂足为O′作AD⊥BC,连接VD,则O′在AD上,
∴∠VDO′为正三棱锥的侧面与底面所成的二面角
设AB=a,VC=b,则
∴b=
R,a=(
-1)R
∴VD=
=
R
∵O′D=
a=
R
∴cos∠VDO′=
=
=
故选A.
∴∠VDO′为正三棱锥的侧面与底面所成的二面角
设AB=a,VC=b,则
|
∴b=
| 2 |
| 3 |
∴VD=
b2-
|
| ||
| 2 |
∵O′D=
| ||
| 6 |
| ||||
| 6 |
∴cos∠VDO′=
| O′D |
| VD |
| ||||||
|
| ||||
| 3 |
故选A.
点评:本题考查面面角,考查学生的计算能力,正确作出面面角,确定AB,VC的关系是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
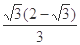 B.
B.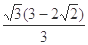
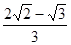 D.
D.