题目内容
(本小题满分12分)把正奇数列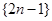 中的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表.设
中的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表.设 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行,从左向右数第
行,从左向右数第 个数.
个数.
(1)若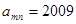 ,求
,求 的值;
的值;
(2)已知函数 的反函数为
的反函数为 ,
, ),若记三角形数表中从上往下数第
),若记三角形数表中从上往下数第 行各数的和为
行各数的和为 .
.
①求数列 的前
的前 项的和
项的和 .
.
②令 设
设 的前
的前 项之积为
项之积为
 ,求证:
,求证:

【答案】
(1) m=45,n=15
(2) 
【解析】(1)∵ ,∴2009是正奇数列的第1005个数.
,∴2009是正奇数列的第1005个数.
前 行共有
行共有 个数,
个数,
前 行共有
行共有 个数.
个数.
∴ .
.
前44行共有 个数.故
个数.故 .
.
(2)①由 ,得
,得 .
.
∵第 行第1个数为
行第1个数为 ,
,
∴ ,∴
,∴ .
.
∴ .
.
 .
.
两式相减,得 ,
,
∴ .
.
② ,
,

即证: .
.
先证: .
.
1° 时,显然成立.
时,显然成立.
2°假设 时,
时, .
.
则 时,
时,


 ,即当
,即当 时,也成立.
时,也成立.
由1°2°知 成立.
成立.
从而


练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目