题目内容
设G为 的重心,过G的直线
的重心,过G的直线 分别交AB,AC于
分别交AB,AC于 ,已知:
,已知: ,
, 和
和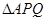 的面积分别为
的面积分别为 ,
,
(Ⅰ) 求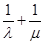 的值; (Ⅱ) 求
的值; (Ⅱ) 求 的取值范围.
的取值范围.
【答案】
(1)3;(2) .
.
【解析】平面几何与解析几何的结合通常涉及到夹角、平行、垂直、共线、轨迹等问题的处理,解决此类问题基本思路是将几何问题坐标化、符号化、数量化,从而将推理转化为运算;或者考虑向量运算的几何意义,利用其几何意义解决有关问题。
解:(Ⅰ)连结AG并延长交BC于M,则M是BC的中点,设 ,则
,则 ,
,
 ①
①
又 ,
②
,
②
 ,
,
 三点共线,故存在实数
三点共线,故存在实数 ,使
,使 ,
,
 ,消
,消 得:
得: ,即
,即 
或者另一种解法由②式得
 , ③
, ③
将③代入①得 .
. 三点共线,
三点共线,
故 ,即
,即  .
.
(Ⅱ) ,
, ,其中
,其中
 ,
, 即
即 ,
,
即  ,
,
其中 时,
时, 有最大值
有最大值 ,
, 时,
时, 有最小值2,
有最小值2,
于是  的取值范围是
的取值范围是 .
.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
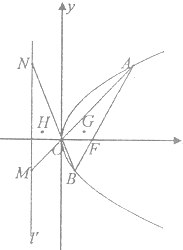 过点F(1,0)的直线l交抛物线C:y2=4x于A,B两点.
过点F(1,0)的直线l交抛物线C:y2=4x于A,B两点.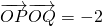 ?若存在,求出直线l的方程,若不存在,说明理由.
?若存在,求出直线l的方程,若不存在,说明理由.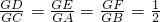 .
. .
. ,
,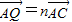 ,试探究:
,试探究: 的值是否为定值,若为定值,求出这个定值;若不是定值,请说明理由.
的值是否为定值,若为定值,求出这个定值;若不是定值,请说明理由.