题目内容
已知函数f(x)=![]() (a>0,a≠1).
(a>0,a≠1).
(1) 证明函数f(x)的图象关于点P(![]() )对称.
)对称.
(2) 令an=![]() ,对一切自然数n,先猜想使an>n2成立的最小自然数a,并证明之.
,对一切自然数n,先猜想使an>n2成立的最小自然数a,并证明之.
(3) 求证:![]() ∈N).
∈N).
证明见解析
解析:
(1)关于函数的图象关于定点P对称, 可采用解几中的坐标证法.
设M(x,y)是f(x)图象上任一点,则M关于P(![]() )的对称点为M’(1-x,1-y),
)的对称点为M’(1-x,1-y),
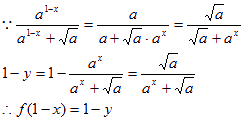
∴M′(1-x,1-y)亦在f(x)的图象上,
故函数f(x)的图象关于点P(![]() )对称.
)对称.
(2)将f(n)、f(1-n)的表达式代入an的表达式,化简可得an=an猜a=3,
即3n>n2.
下面用数学归纳法证明.
设n=k(k≥2)时,3k>k2.
那么n=k+1,3k+1>3·3k>3k2
又3k2-(k+1)2=2(k-![]() )2-
)2-![]() ≥0(k≥2,k∈N)
≥0(k≥2,k∈N)
∴3n>n2.
(3)∵3k>k2
∴klg3>2lgk
令k=1,2,…,n,得n个同向不等式,并相加得:
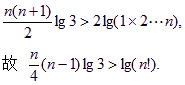

练习册系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|