题目内容
如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( )

- A.相交
- B.平行
- C.异面
- D.以上都有可能
B
试题分析:因为G1,G2分别是△SAB和△SAC的重心,所以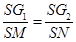 ,所以
,所以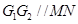 。又因为M、N分别为AB、AC的中点,所以MN//BC,所以
。又因为M、N分别为AB、AC的中点,所以MN//BC,所以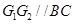 。
。
考点:线面平行的判定定理;线面平行的性质定理;公理4;重心的性质。
点评:我们要掌握重心性质:若G1为△SAB的重心,M为AB中点,则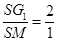 。
。
试题分析:因为G1,G2分别是△SAB和△SAC的重心,所以
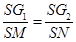 ,所以
,所以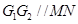 。又因为M、N分别为AB、AC的中点,所以MN//BC,所以
。又因为M、N分别为AB、AC的中点,所以MN//BC,所以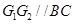 。
。考点:线面平行的判定定理;线面平行的性质定理;公理4;重心的性质。
点评:我们要掌握重心性质:若G1为△SAB的重心,M为AB中点,则
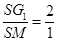 。
。 
练习册系列答案
相关题目
 如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC. 如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( )
如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( ) 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2 (2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( )
(2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( ) (2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )
(2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )