题目内容
已知函数 ,对于下列命题:
,对于下列命题:①函数以f(x)不是周期函数;
②函数f(x)是偶函数;
③对任意x∈R,f(x)满足
 ,其中真命题是 .
,其中真命题是 .
【答案】分析:①由于二次函数不是周期函数,则f(x)不是周期函数
②f(-x)= =f(x),即f(x)是偶函数
=f(x),即f(x)是偶函数
③由于 ,
, ,|4cosπx|≤4,可判断
,|4cosπx|≤4,可判断
解答:解:∵
①由于二次函数不是周期函数,则f(x)不是周期函数,①正确
②f(-x)= =f(x),即f(x)是偶函数,②正确
=f(x),即f(x)是偶函数,②正确
③由于 ,
, ,|4cosπx|≤4
,|4cosπx|≤4
∴|f(x)|=
 ③正确
③正确
故答案为:①②③
点评:本题主要考查了函数的周期性、奇偶性及函数值域的求解,属于函数知识的综合应用.
②f(-x)=
 =f(x),即f(x)是偶函数
=f(x),即f(x)是偶函数③由于
 ,
, ,|4cosπx|≤4,可判断
,|4cosπx|≤4,可判断解答:解:∵

①由于二次函数不是周期函数,则f(x)不是周期函数,①正确
②f(-x)=
 =f(x),即f(x)是偶函数,②正确
=f(x),即f(x)是偶函数,②正确③由于
 ,
, ,|4cosπx|≤4
,|4cosπx|≤4∴|f(x)|=

 ③正确
③正确故答案为:①②③
点评:本题主要考查了函数的周期性、奇偶性及函数值域的求解,属于函数知识的综合应用.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
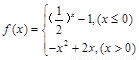 ,对于下列命题:
,对于下列命题: 的最小值是0;
的最小值是0; 上是单调递减函数;
上是单调递减函数; ;
;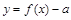 有三个零点,则
有三个零点,则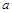 的取值范围是
的取值范围是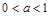 ;
;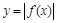 关于直线
关于直线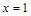 对称.
对称.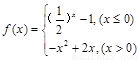 ,对于下列命题:
,对于下列命题: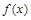 的最小值是0;
的最小值是0;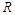 上是单调递减函数;
上是单调递减函数;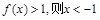 ;
;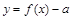 有三个零点,则
有三个零点,则 的取值范围是
的取值范围是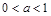 ;
;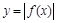 关于直线
关于直线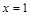 对称.
对称.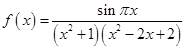 .
.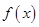 是周期函数;
是周期函数; 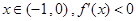 (
(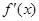 是函数
是函数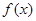 的导函数).
的导函数).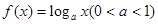 ,对于下列命题:
,对于下列命题: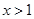 ,则
,则 ; ②若
; ②若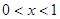 ,则
,则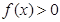 ;
; 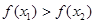 ,则
,则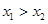 ; ④
; ④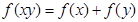 .
.