题目内容
已知函数f(x)=cos(ω•x-θ)(其中ω>0,θ∈[0,π])是奇函数,又函数f(x)的图象关于直线 对称,且在区间(0,
对称,且在区间(0, )内函数f(x)没有零点.
)内函数f(x)没有零点.
(1)求θ和ω的值;
(2)函数f(x)图象是中心对称图形,请写出所有对称中心的坐标;
(3)求函数f(x)的单调递增区间.
解:(1)∵函数f(x)=cos(ω•x-θ)是奇函数,
∴cosθ=0,又θ∈[0,π]),则θ= …2.
…2.
奇函数f(x)的图象关于直线 对称,且在区间(0,
对称,且在区间(0, )内函数f(x)没有零点,
)内函数f(x)没有零点,
则 =
= ,T=
,T= ,
,
∴ω= =6…6
=6…6
(2)函数f(x)=cos(6x- ),由f(x)=0得6x-
),由f(x)=0得6x- =kπ-
=kπ- …7
…7
∴x= (k∈Z).函数f(x)图象的对称中心是(
(k∈Z).函数f(x)图象的对称中心是( ,0),其中k∈Z…9
,0),其中k∈Z…9
(3)f(x)=cos(6x- )=sin6x,
)=sin6x,
∴由2kπ- ≤6x≤2kπ+
≤6x≤2kπ+ 得:
得: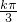 -
- ≤x≤
≤x≤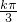 +
+ (k∈Z)…11
(k∈Z)…11
∴函数f(x)的单调递增区间是[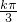 -
- ,
,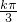 +
+ ](k∈Z)…12
](k∈Z)…12
分析:(1)由f(x)=cos(ω•x-θ)是奇函数,可得f(0)=cosθ=0,又θ∈[0,π],可求得θ,由 =
= ,T=
,T= =
= 可求得ω;
可求得ω;
(2)由(1)可得,f(x)=cos(6x- ),由f(x)=0即可求得其对称中心;
),由f(x)=0即可求得其对称中心;
(3)f(x)=cos(6x- )=sin6x,由2kπ-
)=sin6x,由2kπ- ≤6x≤2kπ+
≤6x≤2kπ+ 可求得函数f(x)的单调递增区间.
可求得函数f(x)的单调递增区间.
点评:本题考查余弦函数的单调性与奇偶性,θ和ω的值的确定是关键,也是难点所在,考查综合分析与转化运用的能力,属于中档题.
∴cosθ=0,又θ∈[0,π]),则θ=
 …2.
…2.奇函数f(x)的图象关于直线
 对称,且在区间(0,
对称,且在区间(0, )内函数f(x)没有零点,
)内函数f(x)没有零点,则
 =
= ,T=
,T= ,
,∴ω=
 =6…6
=6…6(2)函数f(x)=cos(6x-
 ),由f(x)=0得6x-
),由f(x)=0得6x- =kπ-
=kπ- …7
…7∴x=
 (k∈Z).函数f(x)图象的对称中心是(
(k∈Z).函数f(x)图象的对称中心是( ,0),其中k∈Z…9
,0),其中k∈Z…9(3)f(x)=cos(6x-
 )=sin6x,
)=sin6x,∴由2kπ-
 ≤6x≤2kπ+
≤6x≤2kπ+ 得:
得: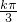 -
- ≤x≤
≤x≤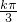 +
+ (k∈Z)…11
(k∈Z)…11∴函数f(x)的单调递增区间是[
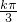 -
- ,
,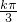 +
+ ](k∈Z)…12
](k∈Z)…12分析:(1)由f(x)=cos(ω•x-θ)是奇函数,可得f(0)=cosθ=0,又θ∈[0,π],可求得θ,由
 =
= ,T=
,T= =
= 可求得ω;
可求得ω;(2)由(1)可得,f(x)=cos(6x-
 ),由f(x)=0即可求得其对称中心;
),由f(x)=0即可求得其对称中心;(3)f(x)=cos(6x-
 )=sin6x,由2kπ-
)=sin6x,由2kπ- ≤6x≤2kπ+
≤6x≤2kπ+ 可求得函数f(x)的单调递增区间.
可求得函数f(x)的单调递增区间.点评:本题考查余弦函数的单调性与奇偶性,θ和ω的值的确定是关键,也是难点所在,考查综合分析与转化运用的能力,属于中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
已知函数f(x)=
,则关于x的方程f2(x)+bf(x)+c=0有5个不同实数解的充要条件是( )
|
| A、b<-2且c>0 |
| B、b>-2且c<0 |
| C、b<-2且c=0 |
| D、b≥-2且c=0 |
 已知函数f(x)的图象如图所示,则函数的值域为( )
已知函数f(x)的图象如图所示,则函数的值域为( )