题目内容
已知二次函数 和“伪二次函数”
和“伪二次函数” 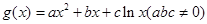 .
.
(Ⅰ)证明:只要 ,无论
,无论 取何值,函数
取何值,函数 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(Ⅱ)在同一函数图像上任意取不同两点A( ),B(
),B( ),线段AB中点为C(
),线段AB中点为C( ),记直线AB的斜率为k.
),记直线AB的斜率为k.
(1)对于二次函数 ,求证
,求证 ;
;
(2)对于“伪二次函数”  ,是否有(1)同样的性质?证明你的结论。
,是否有(1)同样的性质?证明你的结论。
(Ⅰ)恒成立,当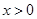 时,
时,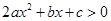 (Ⅱ)恒成立,∵
(Ⅱ)恒成立,∵ ,由二次函数的性质,(Ⅱ)不可能恒成立,则函数
,由二次函数的性质,(Ⅱ)不可能恒成立,则函数 不可能总为增函数.
不可能总为增函数.
(Ⅱ) ;
;
(2)“伪二次函数”  不具有(1)的性质.
不具有(1)的性质.
解析试题分析:(Ⅰ)定义域为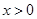 ,如果
,如果 为增函数,则
为增函数,则 (Ⅰ)恒成立,当
(Ⅰ)恒成立,当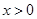 时,
时,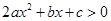 (Ⅱ)恒成立,∵
(Ⅱ)恒成立,∵ ,由二次函数的性质,(Ⅱ)不可能恒成立,则函数
,由二次函数的性质,(Ⅱ)不可能恒成立,则函数 不可能总为增函数. 4分
不可能总为增函数. 4分
(Ⅱ)(1)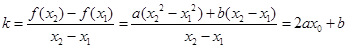 .
.
由  ∴
∴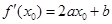 ,则
,则 8分
8分
(2)不妨设 ,对于“伪二次函数”:
,对于“伪二次函数”: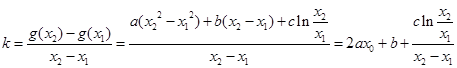 (Ⅲ)
(Ⅲ)
由(1)中(Ⅰ)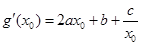 (Ⅳ)
(Ⅳ)
的性质,则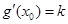 ,比较(Ⅲ)(Ⅳ)两式得
,比较(Ⅲ)(Ⅳ)两式得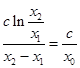 ,
, 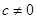
即 (Ⅴ) 令
(Ⅴ) 令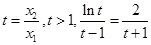 (Ⅵ)
(Ⅵ)
设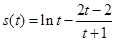 ,则
,则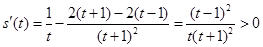
∴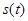 在(1,
在(1, 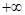 )上递增, ∴
)上递增, ∴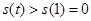
∴(Ⅵ)式不可能成立, (Ⅴ)式不可能成立, 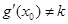
∴“伪二次函数”  不具有(1)的性质. 13分
不具有(1)的性质. 13分
考点:本题主要考查应用导数研究函数的单调性、最值及不等式恒成立问题,不等式的解法。
点评:难题,本题属于导数应用中的基本问题,通过研究函数的单调性,明确了极值情况。(I)中要对a的不同取值情况加以讨论,在解不等式取舍过程中易于出错。涉及不等式恒成立问题,转化成了研究函数的最值,通过构建a的不等式组,求得a的范围。理解“伪函数的概念”的解题的关键之一。

练习册系列答案
相关题目
 .
. 在
在 和
和 处的切线互相平行,求
处的切线互相平行,求 的值;
的值; 的单调区间;
的单调区间; ,若对任意
,若对任意 ,均存在
,均存在 ,使得
,使得 ,求
,求 .
. 的单调性,并说明理由;
的单调性,并说明理由; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 在
在 时有极大值6,在
时有极大值6,在 时有极小值,求
时有极小值,求 的值;并求
的值;并求 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.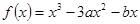 ,其中
,其中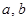 为实数.
为实数.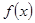 在
在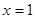 处取得的极值为
处取得的极值为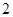 ,求
,求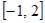 上为减函数,且
上为减函数,且 ,求
,求 的取值范围.
的取值范围. ,其中
,其中 .
. 恒成立,求
恒成立,求 的取值范围;
的取值范围; 的图像上取定两点
的图像上取定两点 ,记直线
,记直线 的斜率为
的斜率为 ,证明:存在
,证明:存在 ,使
,使 成立.
成立.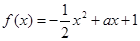 ,
,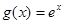 ,
,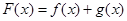 .
.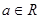
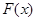 在
在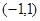 存在极值,求
存在极值,求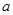 的取值范围;
的取值范围; 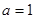 ,问是否存在与曲线
,问是否存在与曲线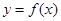 和
和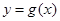 都相切的直线?若存在,判断有几条?并求出公切线方程,若不存在,说明理由。
都相切的直线?若存在,判断有几条?并求出公切线方程,若不存在,说明理由。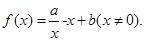 ,其中
,其中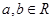
 在点
在点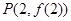 处的切线方程为
处的切线方程为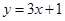 ,求函数
,求函数 的解析式;
的解析式; ,其中
,其中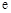 为自然对数的底数.
为自然对数的底数.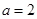 时,求曲线
时,求曲线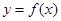 在
在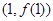 处的切线与坐标轴围成的三角形的面积;
处的切线与坐标轴围成的三角形的面积;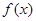 存在一个极大值和一个极小值,且极大值与极小值的积为
存在一个极大值和一个极小值,且极大值与极小值的积为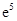 ,求
,求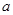 的
的