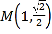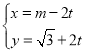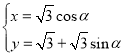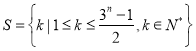题目内容
【题目】在平面直角坐标系![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 满足:直线
满足:直线![]() 与直线
与直线![]() 的斜率之积恒为
的斜率之积恒为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
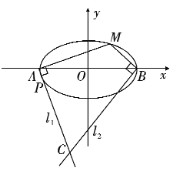
(2)若点![]() 位于第一象限,过点
位于第一象限,过点![]() ,
,![]() 分别作直线
分别作直线![]() ,直线
,直线![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
①若点![]() 的横坐标为-1,求点
的横坐标为-1,求点![]() 的坐标;
的坐标;
②直线![]() 与曲线
与曲线![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)①点
(2)①点![]() 的坐标为
的坐标为![]() ②
②![]()
【解析】
(1)设出动点坐标,根据斜率公式,结合已知可以直接得到曲线![]() 的方程;
的方程;
(2)①设直线![]() 的方程根据已知,可以得到
的方程根据已知,可以得到![]() 的直线方程,解方程组求出
的直线方程,解方程组求出![]() 的坐标,再判断已知的两直线所过的定点,最后求出
的坐标,再判断已知的两直线所过的定点,最后求出![]() 的坐标;
的坐标;
②直线![]() 与曲线
与曲线![]() 的方程联立,根据所给的向量式子,结合根与系数关系最后可以求出
的方程联立,根据所给的向量式子,结合根与系数关系最后可以求出![]() 的取值范围.
的取值范围.
解析:(1)设动点![]() ,由
,由![]()
![]() .
.
(2)①设直线![]() :
:![]() ,
,
由![]() 位于第一象限得
位于第一象限得![]() ,
,
则由![]() ,
,
知![]() ,
,
联立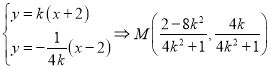 ,
,
由题易得直线![]() 和
和![]() 的方程分别为:
的方程分别为:![]() :
:![]() ,
,![]() :
:![]() .
.
解得其交点![]() 的坐标为
的坐标为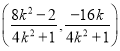 ,由
,由![]() ,解得
,解得![]() ,
,
∵![]() ,∴
,∴![]() .
.
由此可得点![]() 的坐标为
的坐标为![]() .
.
②联立![]() ,
,![]() ,
,
由根与系数的关系有![]()
![]() .
.
由![]()
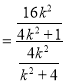
![]() .
.
因为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】为进一步优化教育质量平台,更好的服务全体师生,七天网络从甲、乙两所学校各随机抽取100名考生的某次“四省八校”数学考试成绩进行分析,分别绘制的频率分布直方图如图所示.
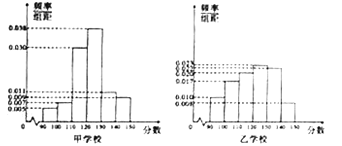
为了更好的测评各个学校数学学科的教学质量,该公司依据每一位考生的数学测试分数将其划分为“![]() ,
,![]() ,
,![]() ”三个不同的等级,并按照不同的等级,设置相应的对学校数学学科教学质量贡献的积分,如下表所示.
”三个不同的等级,并按照不同的等级,设置相应的对学校数学学科教学质量贡献的积分,如下表所示.
测试分数 | 分数对应的等级 | 贡献的积分 |
|
| 1分 |
|
| 2分 |
|
| 3分 |
(1)用样本的频率分布估计总体的频率分布,若将甲学校考生的数学测试等级划分为“![]() 等”和“非
等”和“非![]() 等”两种,利用分层抽样抽取10名考生,再从这10人随机抽取3人,求3人中至少1人数学测试为“
等”两种,利用分层抽样抽取10名考生,再从这10人随机抽取3人,求3人中至少1人数学测试为“![]() 等”的概率;
等”的概率;
(2)视频率分布直方图中的频率为概率,用样本估计总体,若从乙学校全体考生中随机抽取3人,记3人中数学测试等级为“![]() 等”的人数为
等”的人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(3)根据考生的数学测试分数对学校数学学科教学质量贡献的积分规则,分别记甲乙两所学校数学学科质量的人均积分为![]() 和
和![]() ,用样本估计总体,求
,用样本估计总体,求![]() 和
和![]() 的估计值,并以此分析,你认为哪所学校本次数学教学质量更加出色?
的估计值,并以此分析,你认为哪所学校本次数学教学质量更加出色?