题目内容
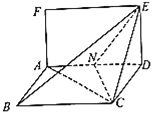
【题目】设
，
，
为两两不重合的平面，
，
，
为两两不重合的直线，给出下列四个命题：
①若
，
，则
；
②若
，
，
，
，则；
③若，
，则
；
④若
，
，
，
，则
.
其中真命题是（ ）
A.①③B.②④C.③④D.①②
【答案】C
【解析】
利用线面垂直的判定定理构造反例，可以判定①错误；根据线面平行的判定定理构造反例，可以判定②错误；利用面面平行和线面平行的定义可以证明③正确；根据线面平行的性质定理和直线的平行公理，可证证明④正确.
对于①：设直线
平面
,当平面
都经过直线a时，
，
，但是
,故①错误；
对于②：当
时，若
，
，
，
，不能得出
，比如当
时,在平面
中任意平行与直线
的两条直线，由线面平行的判定定理可知，成立，
满足条件，但结论不成立，故②错误；
对于③：若，根据平面平行的定义，可知没有公共点，由于
，直线与平面没有公共点，即
，故③正确；
对于④：由
得
，又
,
,∴
，
同理
，故
，故④正确；
故选C.
【题目】为抑制房价过快上涨和过度炒作，各地政府响应中央号召，因地制宜出台了系列房价调控政策.某市拟定出台“房产限购的年龄政策”.为了解人们对“房产限购年龄政策”的态度，在2060岁的人群中随机调查100人，调查数据的频率分布直方图和支持“房产限购”的人数与年龄的统计结果如图所示：
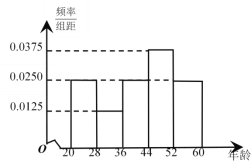
年龄 |
|
|
|
|
|
支持的人数 | 15 | 5 | 15 | 28 | 17 |
（1）由以上统计数据填
列联表，并判断能否在犯错误的概率不超过0.05的前提下认为以44岁为分界点的不同人群对“房产限购年龄政策”的支持度有差异？
44岁以下 | 44岁及44岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
（2）若以44岁为分界点，从不支持“房产限购”的人中按分层抽样的方法抽取8人参加政策听证会，现从这8人中随机抽2人.记抽到44岁以上的人数为
，求随机变量的分布列及数学期望.
参考公式：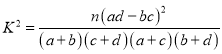
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】盲盒里面通常装的是动漫、影视作品的周边，或者设计师单独设计出来的玩偶．由于盒子上没有标注，购买者只有打开才会知道自己买到了什么，因此这种惊喜吸引了众多年轻人，形成了“盲盒经济”．某款盲盒内可能装有某一套玩偶的
、
、
三种样式，且每个盲盒只装一个．
（1）若每个盲盒装有、、三种样式玩偶的概率相同．某同学已经有了样式的玩偶，若他再购买两个这款盲盒，恰好能收集齐这三种样式的概率是多少？
（2）某销售网点为调查该款盲盒的受欢迎程度，随机发放了200份问卷，并全部收回．经统计，有
的人购买了该款盲盒，在这些购买者当中，女生占
；而在未购买者当中，男生女生各占
．请根据以上信息填写下表，并分析是否有
的把握认为购买该款盲盒与性别有关？
女生 | 男生 | 总计 | |
购买 | |||
未购买 | |||
总计 |
参考公式：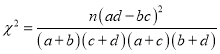
，其中
．
参考数据：
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（3）该销售网点已经售卖该款盲盒6周，并记录了销售情况，如下表：
周数 | 1 | 2 | 3 | 4 | 5 | 6 |
盒数 | 16 | ______ | 23 | 25 | 26 | 30 |
由于电脑故障，第二周数据现已丢失，该销售网点负责人决定用第4、5、6周的数据求线性回归方程，再用第1、3周数据进行检验．
①请用4、5、6周的数据求出
关于
的线性回归方程
；
（注：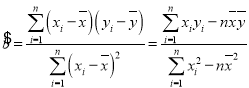
，
）
②若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2盒，则认为得到的线性回归方程是可靠的，试问①中所得的线性回归方程是否可靠？
③如果通过②的检验得到的回归直线方程可靠，我们可以认为第2周卖出的盒数误差也不超过2盒，请你求出第2周卖出的盒数的可能取值；如果不可靠，请你设计一个估计第2周卖出的盒数的方案．
