题目内容
若a，b在区间[0，| 3 |
分析：先利用导数求出函数f（x）=ax3+bx2+ax在R上有两个相异极值点的充要条件，得出关于a，b的约束条件，在a-o-b坐标系中画出可行域，再利用几何概型求出两者的面积比即可．
解答：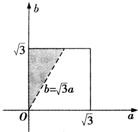
解：易得f′（x）=3ax2+2bx+a，
函数f（x）=ax3+bx2+ax在R上有两个相异极值点的充要条件：
是a≠0且其导函数的判别式大于0，即a≠0且4b2-12a2＞0，
又a，b在区间 [0，
]上取值，则 a＞0，b＞
a，
点（a，b）满足的区域如图中阴影部分所示，
其中正方形区域的面积为3，阴影部分的面积为
，
故所求的概率是
．
故答案为：
．
解：易得f′（x）=3ax2+2bx+a，函数f（x）=ax3+bx2+ax在R上有两个相异极值点的充要条件：
是a≠0且其导函数的判别式大于0，即a≠0且4b2-12a2＞0，
又a，b在区间 [0，
| 3 |
| 3 |
点（a，b）满足的区域如图中阴影部分所示，
其中正方形区域的面积为3，阴影部分的面积为
| ||
| 2 |
故所求的概率是
| ||
| 6 |
故答案为：
| ||
| 6 |
点评：本题主要考查了利用导数研究函数的极值、几何概型．简单地说，如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型．
练习册系列答案
相关题目
若a，b在区间[0，
]上取值，则函数f（x）=ax3+bx2+ax在R上有两个相异极值点的概率是（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、1-
|