题目内容

若数列{a_n}满足a₁= $数学公式$ ，a₁+a₂+…+a_n=n²a_n，则数列{a_n}的前60项和为________．

$\text{[math]}$
分析：根据n≥2时a_n=S_n-S_n-1，算出（n²-1）a_n=（n-1）²a_n-1，得到 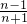$\text{[math]}$ = $\text{[math]}$ ．用累乘的方法算出当n≥2时，a_n= $\text{[math]}$ ，且n=1时也符合条件．由此可得{a_n}的前n项和为和为S_n的表达式，从而得到{a_n}的前60项和的值．
解答：∵数列{a_n}的前n项的和S_n=a₁+a₂+…+a_n，∴S_n=n²a_n，
当n≥2时，S_n-1=（n-1）²a_n-1，两式相减得a_n=n²a_n-（n-1）²a_n-1，
即（n²-1）a_n=（n-1）²a_n-1，故 $\text{[math]}$ = $\text{[math]}$ ，
∴ $\text{[math]}$ = $\text{[math]}$ × $\text{[math]}$ × $\text{[math]}$ ×…× $\text{[math]}$ = $\text{[math]}$ × $\text{[math]}$ ×…× $\text{[math]}$ × $\text{[math]}$ = $\text{[math]}$
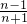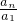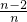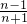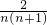
结合a₁= $\text{[math]}$ ，可得a_n= $\text{[math]}$
当n=1时，也满足上式，故a_n= $\text{[math]}$ 对任意n∈N₊成立，
可得a_n= $\text{[math]}$ = $\text{[math]}$ - $\text{[math]}$ ，
因此，数列数列{a_n}的前n项和为S_n=（1- $\text{[math]}$ ）+（ $\text{[math]}$ - $\text{[math]}$ ）+（ $\text{[math]}$ - $\text{[math]}$ ）+…+（ $\text{[math]}$ - $\text{[math]}$ ）=1- $\text{[math]}$ = $\text{[math]}$ ．
∴{a_n}的前60项和为 $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题给出数列{a_n}的前项和S_n与a_n的表达式，求{a_n}的前60项和．着重考查了等差数列的通项公式、数列前n项和S_n与a_n的关系等知识，属于中档题．